| Issue |
Natl Sci Open
Volume 2, Number 3, 2023
Special Topic: Glasses—Materials and Physics
|
|
|---|---|---|
| Article Number | 20220069 | |
| Number of page(s) | 9 | |
| DOI | https://doi.org/10.1360/nso/20220069 | |
| Published online | 28 April 2023 | |
RESEARCH ARTICLE
Granular avalanche statistics in rotating drum with varied particle roughness
1 School of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240, China
2 State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology, Chengdu 610059, China
3 Department of Physics, College of Mathematics and Physics, Chengdu University of Technology, Chengdu 610059, China
* Corresponding authors (emails: yuanyeoct20@sjtu.edu.cn (Ye Yuan); yujiewang@sjtu.edu.cn (Yujie Wang))
Received:
9
December
2022
Revised:
22
February
2023
Accepted:
16
March
2023
We experimentally investigate the avalanche statistics of dry granular materials in a slowly rotating drum for five types of beads with varied surface roughness. For all beads, two distinct angles, i.e., repose angle θr and maximal angle θm, can be clearly defined, and the avalanche size distributions P(δθ) are Gaussian-like. θr, θm, and the span in P(δθ) are all positively correlated with bead surface roughness. This observation thus contrasts with a power-law P(δθ) predicted by self-organized criticality, but is reminiscent of a first-order phase transition. We speculate that both the inertia effect and the velocity-weakening mechanism during an avalanche process can enhance the first-order features, which are however absent in plasticity of sheared amorphous solids. We also discuss the dependence between θr and θm for various particles, as well as the correlation between starting and stopping angles for an individual avalanche.
Key words: granular materials / avalanche / rotating drum
© The Author(s) 2023. Published by Science Press and EDP Sciences
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
INTRODUCTION
Dry granular materials can form mechanically stable piles with a finite slope θ, as a simple manifestation of their particular properties distinct from ordinary phases of matter [1-4]. As θ of a pile slowly increases (by tilting or adding new particles to the top for instance), the surface granular particles start to flow, i.e., an avalanche occurs, and eventually the system will settle into a new θ. One would naturally relate this process to the well-acknowledged self-organized criticality (SOC) based on a sandpile model [5, 6], in the sense that the granular pile self-tunes its θ fluctuating around a potential steady-state value, i.e., a critical point. Specifically for a granular pile in rotating drum, under quasistatic rotation, θ(t) as a function of time behaves as a jagged curve, formed by different linearly increasing intervals punctured by instant drops δθ (i.e., avalanches). In a SOC picture, the avalanche size distribution P(δθ) should be a power law. Although this was partly reproduced in experiments [7, 8], more evidence has refuted SOC for real granular piles since θ(t) displays quasiperiodic feature [9-11]. Two crucial angles can be defined statistically, i.e., maximal angle θm and repose angle θr, before and after an avalanche respectively, which has been documented in early researches [12, 13]. Then one obtains a finite peak Δθ = 〈δθ = θm - θr in P(δθ). Hence the avalanche behavior in granular piles is reminiscent of a first-order phase transition instead of a second-order (SOC) [14]. Comparing the process of increasing θ from θr to θm with that of cooling a liquid in equilibrium, one can associate θr with the freezing point which signals the appearance of nucleus, i.e., locally unstable beads that tend to flow, and θm with the melting point when all nuclei grow to dominate the system, i.e., an avalanche occurs. Alternatively, θm can also be associated with a spinodal point when the situation θr lt; θ lt; θm is considered to be metastable. The incompatibility between first-order and SOC behaviors has been rationalized in different approaches taking into account the flowing dynamics for the surface particles upon the pile during an avalanche [15, 16].
The macroscopic measure θ(t) as well as the debate on first-order or SOC transition can offer insights into vastly different systems far beyond a granular pile. The Coulomb criterion defines the effective friction coefficient μ = tan θ, and thus the fact θm gt; θr can be associated with the hysteresis in solid-fluid transition for stressed granular materials, i.e., one needs a larger shear stress to trigger the flow than to maintain the steady flowing state [3, 2]. Similar velocity-weakening phenomenon is also found in solid friction [17], landslides [18], etc. On the contrary, the stick-slip process of sheared amorphous solids typically possesses a power-law distribution in avalanche size (i.e., stress drop) [19]. A simple model has been proposed to unify the above-mentioned two facets of avalanche statistics [20]. Understanding this issue would benefit the studies on friction law, yielding/plasticity of amorphous materials, and different geophysical processes.
Here we experimentally probe the granular avalanches in a rotating drum, focusing on the macroscopic θ in the quasistatic regime. Despite the easy access of this experiment set-up [2, 11, 21, 22], few studies have clarified the underlying connection between particle properties, macroscopic rheology, and avalanche statistics. Moreover, it has been claimed that microscopic friction should be responsible for the macroscopic hysteresis [23-25], but systematic experiments on θ controlled by friction are lacking to our knowledge. Utilizing the 3D-print technique, we are able to tune the surface roughness of granular beads up to the large friction limit [26, 27], and hence obtain θ for different types of beads with broadly spanning friction. From extensive experiments, we determine two distinct θr and θm for all five beads. Combining with the data in previous literature, we further show a robust linear dependency between θr and θm, irrespective of specific particle properties like surface roughness or shape. We demonstrate that here the avalanche dynamics are more reminiscent of a first-order phase transition and no signature of SOC behaviors is found, since P(δθ) are Gaussian-like for all systems, i.e., θ evolves quasiperiodically as rotated. The detailed correlation between starting and stopping angles for each avalanche event is also studied, which exemplifies the inevitable inertia effect for a particle-level avalanche process.
EXPERIMENTAL DETAILS
As shown in Figure 1A, the cylindrical drum of inner diameter D = 184 mm and width W = 95 mm is attached to the rotary table (KS402-180-5). The rotating drum is driven at different constant angular velocities Ω = 0.1°/s–20°/s. The cylindrical wall is roughened by glueing ABS semispheres of diameter 5–6 mm to avoid the rigid body slipping off the pile. The drum is nearly half filled with different types of beads of diameter d = 2–6 mm (see below). A video camera (Basler acA2040-180 km, 2048×2048 pixels, maximal 180 fps) is installed perpendicularly to the drum plane, such that the plumb line of the granular pile surface can be recorded when rotated. Figure 1B shows an example of the binarized image for the surface profile, from which the angle θ is measured by fitting a straight line to the surface margin. We confirm that this linear profile holds for all Ω covered here.
As illustrated in Figures 1C–1G, we consider spherical beads with five different surface properties, namely steel, ABS, glass, 3D-printed plastic (3DP), and 3D-printed plastic with bumpy surface (BUMP) [26]. They all possess nearly 50:50 bi-dispersity with d = 5/6 mm. Specifically, the BUMP beads in Figure 1G can mimic particles possessing very large friction. Smaller glass beads with d = 2–4 mm are also included to investigate the finite size effect.
 |
Figure 1 (A) Experimental set-up. The cylindrical drum attached to the rotary table is characterized by the diameter D = 184 mm and width W = 95 mm. (B) Binarized image of the pile surface. Red dashed line indicates the linear fit for the margin, from which θ is obtained. (C)–(G) Illustrations of five types of beads, namely steel, ABS, glass, 3D-printed plastic (3DP), and 3D-printed plastic with bumpy surface (BUMP) in sequence. They all possess 50:50 bidisperse diameters d = 5/6 mm. |
QUASISTATIC REGIME
As the drum angular velocity Ω increases, the granular dynamics will crossover from discrete avalanches to continuous flow [28-30]. Figures 2A–2C show the evolution of θ as a function of accumulated rotational angle A = Ωt for three typical Ω. We clearly observe the distinction between (Figure 2A) the jagged curve and (Figure 2C) the fluctuation in continuous flow, as well as (Figure 2B) the intermediate state with moderate Ω. Only for the small-Ω quasistatic regime, discrete avalanches of size δθ can be clearly defined by the instant drop in θ, i.e., δθ = θ2 - θ1, as illustrated in Figure 2A. Statistically, the angles before and after an avalanche respectively define θm and θr, i.e., Δθ = 〈δθ〉= 〈θ2〉- 〈θ1〉= θm - θr.
Notice in Figure 2 we sample θ with a constant Δ A = 0.1° for all Ω, and thus both the average angle Θ = 〈θ〉 (in the quasistatic case Θ = (θm + θr)/2 by definition) and its standard deviation σ(θ) can fairly quantify the dynamic change as Ω grows. Figures 3A and 3B respectively show Θ and σ(θ) as functions of Ω for glass beads in four different sizes, in which the plateaus in Θ and σ(θ) end at different Ω. This is due to the intermediate state (Figure 2B) when the jagged curve (i.e., avalanche regime) is occasionally interrupted by noises, also found in refs. [11, 30]. For this state, Θ varies mildly while σ(θ) decays sharply. Hence the plateau in σ(θ) is the proper indicator for the quasistatic regime, which indicates the persistence of sequential avalanches. In Figure 3B, the locations of Ω when σ decays are varied for different systems. This can be rationalized by the dimensionless Froude number Fr, originally defined by the ratio between two characteristic velocities: v1 = ΩD and  , respectively associated with the external rotation and gravity, i.e.,
, respectively associated with the external rotation and gravity, i.e.,  . Here we note that v1 should be replaced by the free surface velocity scale
. Here we note that v1 should be replaced by the free surface velocity scale  . Since the depth for the surface flow in unit of d would not vary considerably when different beads are used, the downward flux scales as
. Since the depth for the surface flow in unit of d would not vary considerably when different beads are used, the downward flux scales as 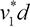 , which simply balances the upward flux caused by rotation ΩD2. This mass conservation gives
, which simply balances the upward flux caused by rotation ΩD2. This mass conservation gives  and thus the modified Froude number is Fr* = Fr·D/d. Figure 3C presents the normalized fluctuation σ/σ0 versus Fr*, in which a clear transition at Fr* = 0.3 is observed, compatible with ref. [11]. As a physical interpretation, the boundary of quasistatic regime means that the time scale for particle restabilization under gravity is comparable to that for lifting a new particle to the top, i.e.,
and thus the modified Froude number is Fr* = Fr·D/d. Figure 3C presents the normalized fluctuation σ/σ0 versus Fr*, in which a clear transition at Fr* = 0.3 is observed, compatible with ref. [11]. As a physical interpretation, the boundary of quasistatic regime means that the time scale for particle restabilization under gravity is comparable to that for lifting a new particle to the top, i.e.,  and v2 are comparable.
and v2 are comparable.
 |
Figure 2 (A)–(C) Evolution of θ as a function of accumulated rotational angle A = Ωt for 5/6 mm ABS beads with Ω = 0.4°/s, 2.8°/s, and 4.8°/s. The vertical dashed line in (A) indicates the definition of an individual avalanche with the size δθ = θ2 - θ1. |
 |
Figure 3 (A) Average angle Θ and (B) its standard deviation σ(Θ) sampled with accumulated angle difference Δ A = 0.1° as a function of Ω for glass beads in four sizes. (C) Rescaled standard deviation σ/σ0 (σ0 refers to σ in the quasistatic limit in (B)) as a function of modified Froude number Fr* = Fr·D/d. Vertical dashed line locates the transition at Fr* = 0.3. |
REPOSE ANGLE AND MAXIMAL ANGLE
In the following, we focus on the measurements for the quasistatic regime. We emphasize that the distinction between θr and θm is not unique for the rotating drum set-up, but reflects the universal features of granular materials. By slowly adding grains to the peak of a heap in which no obstacle exists against the downward flow, clear intermittent avalanches with θr and θm can still be found [29, 31] Θ is positively correlated with the particle size in Figure 3A, reflecting the finite size effect in accordance with refs. [21, 11]. The ratio d/D naturally quantifies the finite size, given that d/W is sufficiently small. For the quasistatic regime in Figure 3A, we plot Θ as a function of d/D in Figure 4A, compared with other results for the similar glass beads [21, 11]. Also included in the inset is the associated angle difference Δθ = θm - θ. Different experiments share a similar trend, i.e., both Θ and Δθ can be extrapolated to finite values as d/D → 0. We also notice that Δθ is relatively robust against different experimental realizations. Physically, the surface properties of glass beads intrinsically determine both the effective friction and the angle hysteresis, which remain finite to the large system size limit. It is then interesting to do a quantitative survey using different types of beads.
At the fixed Ω = 0.4°/s, we investigate the quasistatic avalanches for five types of beads in identical size 5/6 mm (see Figure 1). Their associated θr and θm are listed in Table 1. These angles would possibly shift to lower values if smaller beads are applied due to the finite size effect displayed in Figure 4A. But, considering the identical d/D, the order in θr or θm already indicates the levels of surface roughness for different types of beads. Figure 4B shows θm versus θr for these five beads, along with the data of small glass beads in Figure 4A and granular particles varied in shape or surface properties collected from previous literature [13, 21, 31, 11]. A decent linear relation between θr and θm emerges irrespective of particle properties and experimental details, which has been noted in ref. [21]. Relatively, particles with notable asphericity or surface roughness possess large θr and θm. Furthermore, this relation is weakly ruined by the finite size effect, i.e., our data for different beads of d = 5/6 mm, d/D ≈ 0.03 (solid cubes) slightly deviate from the master curve, while those for small glass beads d/D lt; 0.02 (empty cubes) do not. After checking d/D for all the data in Figure 4B, we choose [θr, θm] with d/D lt; 0.02 to conduct the linear fit (straight line), i.e., θm = 1.256θr - 3.699. This interesting observation indicates that one can inspect both the shape and surface properties of granular particles in a unified approach.
Figure 4C replots θm as a function of Δθ. θm (or θr) are positively correlated with Δθ for our five beads (solid cubes), supporting the view that both the effective friction coefficient and the angle hysteresis are simply monotone increasing functions of microscopic friction coefficient (or surface roughness) for different beads. This can also be inferred from the linear fit in Figure 4B, i.e., by simple algebra one obtains θm = 4.906Δθ + 14.449 (grey line in Figure 4C). According to refs. [23-25], microscopic friction is responsible for a finite angle hysteresis Δθ, and thus the intercept in Figure 4C refers to the finite effective friction when particles are microscopically frictionless. Such reference agrees with that a macroscopic friction exists even for a granular solid composed of frictionless particles due to its particulate nature. However, the value θr = θm ≈ 14° is larger than the prediction ∼ 6° obtained from the simulation of quasistatically sheared frictionless beads [23]. This accurate comparison might suffer from including those aspherical particles for the fit in Figure 4B. Also, the experimental uncertainty in Δθ is not negligible.
 |
Figure 4 (A) Quasistatic average angle Θ as a function of d/D for glass beads, in comparison with the similar results in refs. [21, 11]. Inset shows the associated Δθ as a function of d/D. (B) θm versus θr for five types of beads of d = 5/6 mm (solid cubes). Also included are the data of small glass beads in (A) (empty cubes) as well as previous literature [13, 21, 31, 11]. Straight line indicates the linear fit (see text). (C) θm versus Δθ for the data in (B). Straight line in (B) is also transformed. |
Results of θr and θm for five different beads (d = 5/6 mm)
AVALANCHE STATISTICS
Beyond the sample-averaged measurement, i.e., θr and θm, as discussed above, here we carefully inspect the statistics of individual avalanche events. Figure 5A presents the avalanche size distribution P(δθ) for our five beads, where the five numbers in legend refer to the total numbers of included avalanches for different beads. These five curves share a similar shape, that peaks at a finite δθ, i.e., approximately the average Δθ = 〈δθ〉 considering the probable non-Gaussianity. In Figure 5B, the distributions of the normalized variables ε = (δθ - Δθ)/σ(δθ) for five systems nearly collapse on the normal distribution (curve), and only mild deviations especially at small-ε regime are observed. One probable avenue to inspect the small-δθ regime in Figure 5A is to subtract the Gaussian part from the whole distribution. The remaining part could be associated with SOC behaviors. Considering that the resolution in δθ is estimated by d/D [14], i.e., about 1.7°, and that δθ spans smaller than a decade, avalanche dynamics here displays no meaningful features of SOC. In other words, recalling Figure 2A, the Gaussian-like P(δθ) indicates a quasiperiodic evolution in θ with the quasistatic rotation. Combining with the [θr, θm] data reported above, we obtain a coherent picture that a bead with larger roughness is associated with larger θr, θm, Δθ, as well as a wider span in P(δθ).
As pointed out in ref. [14], the distinguishable θr and θm are reminiscent of the freezing and spinodal points for the supercooled (metastable) branch in a phase diagram. If this view holds accurately, the instant starting and stopping angles θ2 and θ1 should both be narrowly distributed, and their intercorrelation during a single avalanche should be negligible. Figures 6A and 6B respectively show P(θ1) and P(θ2), in which one recognizes that both angles possess Gaussian-like distributions with similar span for each bead. And, P(θ1) and P(θ2) merely show tiny overlaps for any bead, suggesting that our system size is thermodynamically reliable. Like ε in Figure 5B, in Figure 6C, the normalized variables ε1 for θ1 (or ε2 for θ2) are well characterized by the normal distribution. Notice that mild deviations are found for θ1 (solid points), especially for BUMP.
We further check the correlation between θ1 and θ2 for each avalanche event, by calculating the conditional average 〈θ1|θ2〉 as a function of θ2. In order to include all beads, we extract the averages θr and θm from the results, as shown in Figure 6D (y-label is simplified as θ1 - θr). We find that θ1 are negatively correlated with θ2, i.e., a larger instant θ2 tends to be followed by a smaller θ1. The consequent δθ = θ2 - θ1 is positively correlated with θ2, similarly shown in Figure 6E. This consistency can also be proven by the relations θ1 - θr ≈ -0.4(θ2 - θm) and δθ - Δθ ≈ 1.4(θ2 - θm), marked by the straight lines in Figures 6D and 6E. It is reasonable to speculate that the weak correlation between θ1 and θ2 is caused by the specific flowing dynamics, since a larger θ2 accompanies with stronger inertia effect such that the system rests at a smaller θ1 after an avalanche. Accordingly, the span (or standard deviation) of P(δθ) is also larger than that of P(θ1) or P(θ2) because of the above correlation, shown in Figure 6F. Also included are the results for glass beads with d = 2 mm (solid points), and one observes that all three standard deviations approach zero as Δθ → 0. Thus, as bead roughness declines and system size is enlarged, distributions for θ1, θ2, and δθ gradually evolve to delta function with zero average, supplementing Figure 4.
 |
Figure 5 (A) Avalanche size distributions P(δθ) for five types of beads of d = 5/6 mm, with the associated numbers of included avalanche events shown in the legend. (B) Normalized distributions of ε = (δθ - Δθ)/σ(δθ) (σ(δθ) is the standard deviation) for the data in (A). Curve indicates the normal distribution. |
 |
Figure 6 Distributions of individual (A) stopping angle θ1 and (B) starting angle θ for five types of beads of d = 5/6 mm. (C) Normalized distribution of ε1 for θ1 (or ε2 for θ2). Curve indicates the normal distribution. (D) Conditional average of θ1 - θr and (E) δθ - Δθ as functions of the preceding θ2 - θm. Straight lines in (D) and (E) indicate y = -0.4x and y = 1.4x, respectively. (F) Standard deviations of P(δθ), P(θ1), and P(θ2) as functions of Δθ. Solid points refer to the results of glass beads of d = 2 mm. |
DISCUSSION
In this work, we experimentally investigate the avalanche statistics in a quasistatically rotating drum for five types of beads with varied surface roughness (or friction coefficient as the ideal equivalence). The evolution of granular pile slope θ allows one to define the starting and stopping angles θ2, θ1, before and after an avalanche event, respectively. In the average meaning, both the repose and maximal angles (θr = 〈θ1 and θm = 〈θ2), as well as their difference Δθ which quantifies the hysteresis, are all positively correlated with the bead roughness. One could further infer the extreme situation for frictionless granular particles, possessing no hysteresis but a finite slope (i.e., macroscopic effective friction). The avalanche size (i.e., δθ = θ2 - θ1) distributions P(δθ) are Gaussian-like for all beads, indicating that θ evolves quasiperiodically and thus the avalanche dynamics in rotating drum is a first-order transition rather than SOC irrespective of specific bead roughness. We also show the weak correlation between θ1 and θ2 (also δθ), i.e., a larger θ2 tends to be followed by a smaller θ1, suggesting the inertia effect.
The original sandpile model for SOC [5] has not included the inertia effect involved in a real granular avalanche. Also, the velocity-weakening in either microscopic or macroscopic (effective) friction [15] should be taken into account for an initiated flow. Therefore, for our rotating drum, once θm is exceeded, an avalanche occurs and both the above factors (they are not necessarily independent) lead to a restabilized angle smaller than θm, i.e., θr which even strongly depends on θm. This contrasts with a single critical point as expected based on SOC. However, by slowly adding particles to a pile, SOC behaviors can still be reproduced since now avalanche is achieved not catastrophically but in a quasistatic manner [8], i.e., a clear θr is forbidden. Alternatively, introducing mechanical perturbation would destabilize a pile before θm is reached, also resulting in a SOC domain [32]. All these considerations indicate that the competition between SOC and first-order transition is considerably affected by the driving protocols for granular avalanches on the particle level. On the contrary, the stress avalanche statistics in quasistatically sheared amorphous solids display notable agreement with the SOC prediction [19]. This indicates that avalanches on particle and contact levels should be treated differently. A unified framework to explain the above rich phenomena is still a hot topic [20]. Any progress in this direction will benefit the understanding of granular constitutive law, plasticity of amorphous solids, and related geophysical processes like landslides and earthquakes.
Funding
Y.Y. acknowledges support from the fellowship of China Postdoctoral Science Foundation (2021M702151). This work was supported by the National Natural Science Foundation of China (11974240) and the Science and Technology Commission of Shanghai Municipality (22YF1419900).
Author contributions
Y.W. conceived the concept. A.P. carried out the experiments. A.P., Y.Y., and Y.W. analyzed the data and wrote the paper.
Conflict of interest
The authors declare no conflict of interest.
References
- Jaeger HM, Nagel SR, Behringer RP. Granular solids, liquids, and gases. Rev Mod Phys 1996; 68: 1259–1273. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Forterre Y, Pouliquen O. Flows of dense granular media. Annu Rev Fluid Mech 2008; 40: 1–24. [Article] [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Andreotti B, Forterre Y, Pouliquen O. Granular Media: Between Fluid and Solid. Cambridge: Cambridge University Press, 2013. [CrossRef] [Google Scholar]
- Kou B, Cao Y, Li J, et al. Granular materials flow like complex fluids. Nature 2017; 551: 360–363. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bak P, Tang C, Wiesenfeld K. Self-organized criticality. Phys Rev A 1988; 38: 364–374. [Article] [Google Scholar]
- Turcotte DL. Self-organized criticality. Rep Prog Phys 1999; 62: 1377–1429. [Article] [CrossRef] [Google Scholar]
- Frette V, Christensen K, Malthe-Sørenssen A, et al. Avalanche dynamics in a pile of rice. Nature 1996; 379: 49–52. [Article] [CrossRef] [Google Scholar]
- Ramos O, Altshuler E, Måløy KJ. Avalanche prediction in a self-organized pile of beads. Phys Rev Lett 2009; 102: 078701. [Article] [CrossRef] [PubMed] [Google Scholar]
- Jaeger HM, Liu CH, Nagel SR. Relaxation at the angle of repose. Phys Rev Lett 1989; 62: 40–43. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fischer R, Gondret P, Perrin B, et al. Dynamics of dry granular avalanches. Phys Rev E 2008; 78: 021302. [Article] [CrossRef] [PubMed] [Google Scholar]
- Balmforth NJ, McElwaine JN. From episodic avalanching to continuous flow in a granular drum. Granul Matter 2018; 20: 52. [Article] [Google Scholar]
- Bagnold RA. The shearing and dilatation of dry sand and the “singing" mechanism. Proc Royal Soc London Ser A Math Phys Sci 1966; 295: 219. [NASA ADS] [Google Scholar]
- Carrigy MA. Experiments on the angles of repose of granular materials. Sedimentology 1970; 14: 147–158. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Nagel SR. Instabilities in a sandpile. Rev Mod Phys 1992; 64: 321–325. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Jaeger HM, Liu CH, Nagel SR, et al. Friction in granular flows. Europhys Lett 1990; 11: 619–624. [Article] [CrossRef] [Google Scholar]
- Bouchaud JP, Cates ME, Prakash JR, et al. Hysteresis and metastability in a continuum sandpile model. Phys Rev Lett 1995; 74: 1982–1985. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Baumberger T, Caroli C. Solid friction from stick-slip down to pinning and aging. Adv Phys 2006; 55: 279–348. [Article] [CrossRef] [Google Scholar]
- Jerolmack DJ, Daniels KE. Viewing Earth's surface as a soft-matter landscape. Nat Rev Phys 2019; 1: 716–730. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Nicolas A, Ferrero EE, Martens K, et al. Deformation and flow of amorphous solids: Insights from elastoplastic models. Rev Mod Phys 2018; 90: 045006. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Dahmen KA, Ben-Zion Y, Uhl JT. A simple analytic theory for the statistics of avalanches in sheared granular materials. Nat Phys 2011; 7: 554–557. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Liu XY, Specht E, Mellmann J. Experimental study of the lower and upper angles of repose of granular materials in rotating drums. Powder Tech 2005; 154: 125–131. [Article] [CrossRef] [Google Scholar]
- Gray JMNT. Particle segregation in dense granular flows. Annu Rev Fluid Mech 2018; 50: 407–433. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Peyneau PE, Roux JN. Frictionless bead packs have macroscopic friction, but no dilatancy. Phys Rev E 2008; 78: 011307. [Article] [CrossRef] [PubMed] [Google Scholar]
- DeGiuli E, Wyart M. Friction law and hysteresis in granular materials. Proc Natl Acad Sci USA 2017; 114: 9284–9289. [Article] [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Perrin H, Clavaud C, Wyart M, et al. Interparticle friction leads to nonmonotonic flow curves and hysteresis in viscous suspensions. Phys Rev X 2019; 9: 031027. [Article] [NASA ADS] [Google Scholar]
- Yuan Y, Xing Y, Zheng J, et al. Experimental test of the edwards volume ensemble for tapped granular packings. Phys Rev Lett 2021; 127: 018002. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zeng Z, Zhang S, Zheng X, et al. Equivalence of fluctuation-dissipation and Edwards’ temperature in cyclically sheared granular systems. Phys Rev Lett 2022; 129: 228004. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rajchenbach J. Flow in powders: From discrete avalanches to continuous regime. Phys Rev Lett 1990; 65: 2221–2224. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lemieux PA, Durian DJ. From avalanches to fluid flow: a continuous picture of grain dynamics down a heap. Phys Rev Lett 2000; 85: 4273–4276. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fischer R, Gondret P, Rabaud M. Transition by intermittency in granular matter: from discontinuous avalanches to continuous flow. Phys Rev Lett 2009; 103: 128002. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Börzsönyi T, Halsey TC, Ecke RE. Avalanche dynamics on a rough inclined plane. Phys Rev E 2008; 78: 011306. [Article] [CrossRef] [PubMed] [Google Scholar]
- Evesque P, Rajchenbach J. Instability in a sand heap. Phys Rev Lett 1989; 62: 44–46. [Article] [Google Scholar]
All Tables
All Figures
 |
Figure 1 (A) Experimental set-up. The cylindrical drum attached to the rotary table is characterized by the diameter D = 184 mm and width W = 95 mm. (B) Binarized image of the pile surface. Red dashed line indicates the linear fit for the margin, from which θ is obtained. (C)–(G) Illustrations of five types of beads, namely steel, ABS, glass, 3D-printed plastic (3DP), and 3D-printed plastic with bumpy surface (BUMP) in sequence. They all possess 50:50 bidisperse diameters d = 5/6 mm. |
| In the text | |
 |
Figure 2 (A)–(C) Evolution of θ as a function of accumulated rotational angle A = Ωt for 5/6 mm ABS beads with Ω = 0.4°/s, 2.8°/s, and 4.8°/s. The vertical dashed line in (A) indicates the definition of an individual avalanche with the size δθ = θ2 - θ1. |
| In the text | |
 |
Figure 3 (A) Average angle Θ and (B) its standard deviation σ(Θ) sampled with accumulated angle difference Δ A = 0.1° as a function of Ω for glass beads in four sizes. (C) Rescaled standard deviation σ/σ0 (σ0 refers to σ in the quasistatic limit in (B)) as a function of modified Froude number Fr* = Fr·D/d. Vertical dashed line locates the transition at Fr* = 0.3. |
| In the text | |
 |
Figure 4 (A) Quasistatic average angle Θ as a function of d/D for glass beads, in comparison with the similar results in refs. [21, 11]. Inset shows the associated Δθ as a function of d/D. (B) θm versus θr for five types of beads of d = 5/6 mm (solid cubes). Also included are the data of small glass beads in (A) (empty cubes) as well as previous literature [13, 21, 31, 11]. Straight line indicates the linear fit (see text). (C) θm versus Δθ for the data in (B). Straight line in (B) is also transformed. |
| In the text | |
 |
Figure 5 (A) Avalanche size distributions P(δθ) for five types of beads of d = 5/6 mm, with the associated numbers of included avalanche events shown in the legend. (B) Normalized distributions of ε = (δθ - Δθ)/σ(δθ) (σ(δθ) is the standard deviation) for the data in (A). Curve indicates the normal distribution. |
| In the text | |
 |
Figure 6 Distributions of individual (A) stopping angle θ1 and (B) starting angle θ for five types of beads of d = 5/6 mm. (C) Normalized distribution of ε1 for θ1 (or ε2 for θ2). Curve indicates the normal distribution. (D) Conditional average of θ1 - θr and (E) δθ - Δθ as functions of the preceding θ2 - θm. Straight lines in (D) and (E) indicate y = -0.4x and y = 1.4x, respectively. (F) Standard deviations of P(δθ), P(θ1), and P(θ2) as functions of Δθ. Solid points refer to the results of glass beads of d = 2 mm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.

