Optimal coordination of zero carbon building energy systems

Special Topic: Energy Systems of Low Carbon Buildings

Open Access

Algorithm 1

Seasonal-daily scheduling approach

Step 1. Initialize. Set system device capacity as

{P^{PV}, P^{EL}, P^{FC}, P^{HP}, P^{EB}, M^{HS}, G^{HW}, Q^{CW}}

, get renewable generation and demand uncertainty sets as

{\hat{S_{t}}, {\hat{p}}_{t}^{DE}, {\hat{g}}_{t}^{DE}, {\hat{q}}_{t}^{DE}, \forall t}

and

{∆ S_{t}, ∆ p_{t}^{DE}, ∆ g_{t}^{DE}, ∆ q_{t}^{DE}, \forall t}

. Set current energy storage status as

{m_{1}^{HS}, g_{1}^{HW}, q_{1}^{CW}}

, set seasonal scheduling period Y and daily scheduling period D. Set seasonal scheduling counts k = 1.
Step 2. Optimal seasonal robust scheduling. Seasonal scheduling aims to achieve optimal annual operation costs by minimizing the annual hydrogen purchase considering both the renewable generation and demand uncertainty in the worst case. Consider there are N days in the current month, set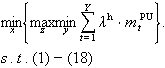

k = k + 1

and calculate the optimization problem as

\begin{array}{l} \min_{x} {\max_{z} \min_{y} \sum_{t = 1}^{Y} λ^{h} \cdot m_{t}^{PU}} . \\ s . t . (1) - (18) \end{array}

(24)
Optimal Then optimal robust scheduling problem is solved by C&CG and commercial solver, the seasonal storage scheduling as

{{\bar{m}}_{k}^{HS, M}, {\bar{g}}_{k}^{GW, M}}

is obtained. Set daily scheduling counts

d = 1

.
Step 3. Optimal daily economic scheduling. The objective of daily scheduling is to minimize operation costs while adhering to the seasonal storage scheduling strategy. With the current energy storage status represented as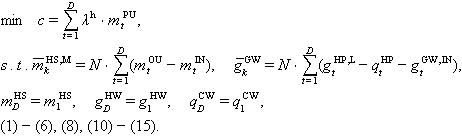

{m_{1}^{HS}, g_{1}^{HW}, q_{1}^{CW}}

and daily renewable and demand forecasting as

{p_{t}^{DE}, g_{t}^{DE}, q_{t}^{DE}, S_{t}, \forall t}

, the optimization problem can be formulated as follows:

\begin{array}{l} \min c = \sum_{t = 1}^{D} λ^{h} \cdot m_{t}^{PU}, \\ s . t . {\bar{m}}_{k}^{HS, M} = N \cdot \sum_{t = 1}^{D} (m_{t}^{OU} - m_{t}^{IN}), {\bar{g}}_{k}^{GW} = N \cdot \sum_{t = 1}^{D} (g_{t}^{HP, L} - q_{t}^{HP} - g_{t}^{GW, IN}), \\ m_{D}^{HS} = m_{1}^{HS}, g_{D}^{HW} = g_{1}^{HW}, q_{D}^{CW} = q_{1}^{CW}, \\ (1) - (6), (8), (10) - (15). \end{array}

(25)
The daily scheduling problem can be solved by a commercial solver, and all decision variables are obtained as part of the daily scheduling strategy. Then set

d = d + 1

and output the daily scheduling.
Step 4. Check stopping criteria. If

s ⩾ Y

, a seasonal-daily operation is complete, the scheduling stops and exits. Else, if

d ⩾ N

, the monthly scheduling is finished, and the process returns to Step 2 for the next seasonal scheduling. Otherwise, go to Step 3 and solve the subsequent daily scheduling.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.