Dissipative gap solitons and vortices in moiré optical lattices

Li Wang; Zhenya Yan; Yi Zhu; Jianhua Zeng

doi:10.1360/nso/20240011

All issues

Volume 3 / No 6 (2024)

Natl Sci Open, 3 6 (2024) 20240011

Full HTML

Open Access

Issue		Natl Sci Open Volume 3, Number 6, 2024


Article Number		20240011
Number of page(s)		13
Section		Physics
DOI		https://doi.org/10.1360/nso/20240011
Published online		28 June 2024

National Science Open 3: 20240011, 2024

RESEARCH ARTICLE

Dissipative gap solitons and vortices in moiré optical lattices

Li Wang¹^,2^,3, Zhenya Yan⁴^,5, Yi Zhu²^,3 and Jianhua Zeng¹^,6^,7^*

¹ Center for Attosecond Science and Technology, State Key Laboratory of Transient Optics and Photonics, Xi’an Institute of Optics and Precision Mechanics of Chinese Academy of Sciences, Xi’an 710119, China
² Yau Mathematical Sciences Center and Department of Mathematics, Tsinghua University, Beijing 100084, China
³ Beijing Institute of Mathematical Sciences and Applications, Beijing 101408, China
⁴ Key Lab of Mathematics Mechanization, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China
⁵ School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
⁶ School of Optoelectronics, University of Chinese Academy of Sciences, Beijing 100049, China
⁷ Collaborative lnnovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

^* Corresponding author (email: zengjh@opt.ac.cn)

Received: 14 April 2024
Revised: 9 June 2024
Accepted: 11 June 2024

Abstract

Considerable attention has been recently paid to elucidation the linear, nonlinear and quantum physics of moiré patterns because of the innate extraordinary physical properties and potential applications. Particularly, moiré superlattices consisted of two periodic structures with a twist angle offer a new platform for studying soliton theory and its practical applications in various physical systems including optics, while such studies were so far limited to reversible or conservative nonlinear systems. Herein, we provide insight into soliton physics in dissipative physical settings with moiré optical lattices, using numerical simulations and theoretical analysis. We reveal linear localization-delocalization transitions, and find that such nonlinear settings support plentiful localized gap modes representing as dissipative gap solitons and vortices in periodic and aperiodic moiré optical lattices, and identify numerically the stable regions of these localized modes. Our predicted dissipative localized modes provide insightful understanding of soliton physics in dissipative nonlinear systems since dissipation is everywhere.

Key words: moiré optical lattices / dissipative gap solitons and vortices / localization-delocalization transition / dissipation and gain / self-defocusing nonlinearity

© The Author(s) 2024. Published by Science Press and EDP Sciences.

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

INTRODUCTION

Solitons are pervasive self-trapped nonlinear localized patterns existing in diverse branches of disciplines including physics, optics, mathematics, biology, etc. [1]. The elegant balance between dispersion/diffraction (or their combination) and nonlinearity results in the formation of solitons which own three unique properties: (i) shape-preservation; (ii) constant velocity during the propagation; (iii) unchanged amplitude, shape and velocity during a soliton collision. In nonlinear optics, such a self-trapped nonlinear phenomenon is called optical solitons—laser wavepackets that do not diverge when the two effects, dispersion/diffraction and self-focusing or defocusing Kerr nonlinearity, are compatible with each other. Remarkably, the optical soliton research has attracted sustained enthusiasm of scientists during the past five decades, and is welcoming its bright prospects for fundamental research and potential applications in the decades to come [2-4].

The formation, structural property, and dynamical mechanisms are among the three essential and significant elements in soliton research; to better control such three elements, linear strategies and nonlinear ones are usually taken [2-4]. New soliton physics were revealed in nonlinear physical systems with periodic potentials such as photonic crystals/lattices in optics and optical lattices in Bose-Einstein condensates in the past years [5-14]. Particularly, new spatially localized structures called bright gap solitons and their vortical counterparts (vortex gap solitons carried with topological charge) [5, 6, 9-14], dark gap solitons and vortices [7, 8] within the finite gaps of the underlying linear Bloch spectrum, can even be excited under the self-defocusing nonlinearity, enabling the existence of stable localized gap modes through combing the band gap engineering and materials’ nonlinear effects in such nonlinear periodic systems. The zealous pursuit of waves manipulation by simply building the structures of two-dimensional materials, profound linear, nonlinear and quantum effects and dynamics supported by moiré lattices are popping up in different branches of physics spanned from condensed matter physics to optics and ultracold atomic gases [15-25]. Among these topics, the soliton research is unfolding in various physical systems with moiré lattices [15, 17, 18, 26-34], while such studies are all about conservative systems.

Dissipation is commonly unavoidable in nonconservative physical systems, and therefore, methods to compensate energy should be introduced. If the dissipation is balanced by gain, and the dispersion/diffraction is harmonious with surrounding nonlinearity, then we could have dissipative solitons [8, 13, 35-41]. Accordingly, the underlying physics (concept) and formation mechanism of dissipative solitons are very different from that of optical solitons in conservative systems as mentioned above. In last years, various dissipative solitons have been experimentally confirmed in different physics contexts [41-47], such as high-energy dissipative solitons and breathing ones in mode-locked fiber lasers [42, 43] and dissipative solitons in multimode fiber lasers [44] have been created, optomechanical dissipative solitons in an optomechanical microresonator were observed [45], and dissipative Kerr solitons [46] and Kerr-soliton combs [47] in optical microresonators were reported. Theoretically, several useful schemes have been applied to the formation and stabilization of dissipative solitons [48]. For multidimensional dissipative solitons, a recent reviewed article summarizes the present results in nonlinear dissipative media [48].

In this article, we theoretically and numerically address the formation and stability properties of dissipative gap solitons and vortices in a two-dimensional nonlinear dissipative medium with moiré optical lattices, nonlinear absorption (loss caused by two-photon absorption) and linear gain. We reveal the linear properties of such moiré lattices under different twisted angles by presenting the underlying linear band gap structures in momentum space, density of states, linear Bloch functions, eigenmodes and the associated form-factors, demonstrating the extremely flat Bloch bands and localization-delocalization transition (LDT) of light. The stability regions of localized gap modes within the finite gaps are identified via perturbed direct simulations. The predicted linear and nonlinear localization features of the physical model with commensurate (periodic) and incommensurate (aperiodic) moiré optical lattices enlighten us a new avenue of light-field manipulation in dissipative media and how to achieve that goal.

RESULTS

Theoretical model

We consider the nonlinear propagation of laser light in a defocusing cubic (Kerr) medium with transverse shallow refractive index distribution configured as a moiré optical lattice, with two-photon absorption and linear gain. 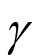The propagation dynamics along propagation distance $z$ in such system is governed by the generalized nonlinear Schrödinger (NLS) equation for light field amplitude $Ψ$ : $i \frac{\partial Ψ}{\partial z} = - \frac{1}{2} \nabla^{2} Ψ + V_{OL} Ψ + {| Ψ |}^{2} Ψ + i γ Ψ - i α {| Ψ |}^{2} Ψ,$ (1)where Lapalacian $\nabla^{2} = \partial^{2} / \partial x^{2} + \partial^{2} / \partial y^{2}$ ; $γ$ represents the transverse gain coefficient; and $α$ accounts for two-photon absorption. The 2D moiré optical lattices, consisted of two uniform square lattices with a twisted angle $θ$ , yield $V_{OL} = V_{0} - [V_{1} {(cos x + cos y)}^{2} + V_{2} {(cos x^{'} + cos y^{'})}^{2}],$ (2)where we define V₀=18 and the modulation depth (strength) of the two optical lattices with periodicity π, V₁=V₂=2.2, for discussion otherwise stated. The transformation of cartesian coordinates system between $(x, y)$ plane and the $(x^{'}, y^{'})$ plane is defined by a rotating angle θ: $\begin{array}{l} (\begin{matrix} x^{'} \\ y^{'} \end{matrix}) = (\begin{matrix} \cos (θ), - \sin (θ) \\ \sin (θ), \cos (θ) \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) . \end{array}$ (3)We here devote our attention to the moiré optical lattices of the square type, particularly one can get the normal untwisted square lattice from Eq. (2) by simply setting V₂=0 or θ=0. A unique feature of the moiré pattern with very shallow lattice strength is to introduce the twisted angle (rotating) freedom degree and structuring 2D configurable synthetic structures enabling band-gap engineering and finally the molding flow of light almost by will. By altering the value of the rotating angle θ, the moiré optical lattices would undergo alternate changes from commensurate (periodic) to incommensurate (aperiodic) configurations which, however, always keeps the extremely flat bands properties. The commensurate case is based on the fact that under the context of Pythagorean angles $θ = \arctan (b / a)$ , with $\cos θ = a / c, \sin θ = b / c$ , and natural numbers $(a, b, c)$ constitute Pythagorean triples, $a^{2} + b^{2} = c^{2}$ , the moiré optical lattices are virtually considered as the elementary square Bravais lattices.

The stationary solitary-wave solution $Φ$ under propagation constant b can be constructed as $Ψ = Φ e^{ib z}$ , after substituting it into the dynamical fundamental equation (Eq. (1)), one can get the stationary equation: $b Φ = \frac{1}{2} \nabla^{2} Φ - V_{OL} Φ - {| Φ |}^{2} Φ - i γ Φ + i α {| Φ |}^{2} Φ .$ (4)Equation (4) holds the power $P = \int \int | Φ |^{2} d x d y$ .

Linear Bloch-wave spectrum

We first consider the linear Bloch-wave structure of the physical model (Eq. (4)) by dropping the last three terms. As mentioned above, for commensurate moiré optical lattices with elementary square Bravais lattices (such configuration is also known as Pythagorean lattices) under the context of Pythagorean angles θ, we can easily produce their band gap diagram upon employing the commonly used linear Bloch band-gap theory. For the incommensurate moiré optical lattices wherein θ is now non-Pythagorean, the periodic potential can be approximated by an almost periodic function based on the effective-cell approach and then we have an incommensurable almost periodic lattice; in other words, we can use an effective Pythagorean lattice to replace the original incommensurate (non-Pythagorean) moiré lattice by finding a Pythagorean triplet with a larger natural numbers (a, b, c), according to a recent foundational work [16]. It is therefore one can produce the linear Bloch-wave structures of moiré optical lattices under arbitrarily angle θ.

Depicted in the first column of Figure 1 are the contour plots of such moiré lattices under both the commensurate and incommensurate cases, and in the second column are their corresponding band-gap spectra in the reciprocal lattice momentum space. Specifically, the commensurate moiré lattices under Pythagorean angles θ=arctan(3/4), θ=arctan(5/12) and θ=arctan(8/15) are respectively displayed in Figure 1(a1), (b1) and (c1), whereas the incommensurate one for non-Pythagorean twisted angle θ=π/4 is in Figure 1(d1); these 2D twisted configurable structures could produce many extremely flat Bloch bands which are unique for moiré patterns, according to their associated Bloch-wave spectra in Figure 1(a2), (b2), (c2) and (d2). The empty spaces between these abundant flat Bloch bands are the finite gaps where the propagation of waves is forbidden on account of strong Bragg scattering, the finite gaps could open wider for commensurate moiré lattices and narrower for incommensurate counterpart (comparing Figure 1(a2), (b2) and (c2) to Figure 1(d2)). We have also shown the photonic density of states of these moiré lattices in the third column of Figure 1, displaying a well match with their band gap structures; it is also see that the maximum power of light is not always appear on the first Bloch band. To elucidate more details of the underlying linear Bloch band properties, we present the first four linear Bloch waves of the commensurate moiré lattice under Pythagorean angle θ=arctan(8/15) (Figure 1(c1)) in the fourth column of Figure 1, showing that the structures of linear Bloch waves change drastically (Figure 1(a4), (b4) and to Figure 1(c4), (d4)). We emphasize that the linear Bloch waves own very similar spatial structures for incommensurate moiré lattice (not shown here).

Figure 1

The contour structures (first column) of 2D moiré optical lattices and the associated band-gap spectra (second column), photonic density of states (third column), the linear Bloch-wave within one unit cell. Contour geometries of periodic (a1, b1, c1) and aperiodic (d1) moiré optical lattices under different twisted angle: (a1) θ=atan(3/4), (b1) θ=atan(5/12), (c1) θ=atan(8/15), and (d1) θ=π=4. The associated band-gap spectra in the reciprocal lattice momentum space (a2, b2, c2, d2) and the photonic density of states (a3, b3, c3, d3). The first four linear Bloch waves (within a primitive lattice cell) of the moiré optical lattice under θ=atan(8/15). Yellow arrows in (a1, b1, c1) denote the primitive lattice vectors.

Linear localization-delocalization transition (LDT)

To illustrate the influence of the sublattices strength and rotating angle θ on the linear localization of light, we search the linear spatial eigenmodes of the moiré lattice as $Ψ = Φ e^{ib z}$ through the linearized Eq. (4) by abandoning the nonlinear terms and linear gain one (last three terms). According to Ref. [16], we define the integral form-factor as $χ = (P^{- 2} \int \int | Φ |^{4} d x d y)^{1 / 2}$ (here $P = \int \int | Φ |^{2} d x d y$ as given above), and calculate its value of the most localized modes (the modes with the largest propagation constant b) depended on the rotating angle θ and sublattice depth V₂ and show such dependence in Figure 2(a). Under the given conditions of V₀=18 and V₁=0.1 (the first sublattice’s depth), one can see from the figure that there is a sudden LDT of light when the depth of the second sublattice becomes larger than its threshold $V_{2} > V_{2}^{LDT} \approx 1.42$ , and notably, such linear LDT of light (and then the formation of localized linear eigenmodes) arises only for aperiodic moiré optical lattices with non-Pythagorean twisted angles θ, while the linear eigenmodes are alway delocalized for periodic moiré lattices with arbitrarily Pythagorean angles θ, which lead to the appearance of dips in $χ (V_{2}, θ)$ dependency relationship. Schematic eigenmodes below and above the LDT threshold are respectively depicted in Figure 2(b) and (c), showing the delocalized mode and localized one. The localized mode above LDT threshold can be understood by the linear Bloch band flattening of the incommensurate moiré optical lattices which are approximated as almost periodic Pythagorean lattices under the condition of $V_{2} > V_{2}^{LDT}$ .

Figure 2

(a) Form-factor χ of the linear eigenmode of a moiré optical lattice with the largest propagation constant versus θ and V₂ at V₁=0.1. Yellow dashed lines present the commensurate (periodic) moiré lattices under some of the Pythagorean angles (from left to right) θ=atan(13/84), atan(5/12), atan(8/15), atan(3/4), atan(20/21), and atan(4/3). Eigenmode profiles $| Φ |$ with the largest propagation constant supported by a incommensurate (aperiodic) moiré lattice under twisted non-Pythagorean angle θ=π/4 and with V₁=0.1 for different V₂ values: V₂₌0.6 (b) and V₂=1.6 (c).

Fundamental dissipative gap solitons

Having obtained the linear Bloch-wave spectra of the moiré optical lattices under consideration, we now switch to consider the existence, property and dynamical process of the fundamental-type nonlinear localized gap modes called fundamental gap solitons situated within the first finite gap (of such linear spectra). We firstly investigate the formation of the localized gap mode in commensurate moiré optical lattices since which exhibit a very wide first gap, which is an advantageous prerequisite for exciting gap solitons. The fundamental dissipative gap solitons families manifested by dependencies of soliton power P on propagation constant b in a periodic moiré lattice with Pythagorean triples (3, 4, 5) (corresponding to the Pythagorean angle θ=arctan(3/4)) are summed in Figure 3(a). The curve P(b) shows a well agreement with the inverted Vakhitov-Kolokolov stability criterion dP/db<0, an indispensable but not a sufficient condition for judging the stability of gap solitons in defocusing nonlinear media [7-12, 31-33, 49]. Detailed insight into such stability and instability of dissipative gap solitons through direct perturbed numerical simulations, we conclude that the solitons are stable in the midst of finite gap, while are unstable close to the band edge, as displayed by solid line and dashed one in Figure 3(a). The characterized examples of an unstable gap soliton and a stable one, marked by points A and B in Figure 3(a), are shown in Figure 3(c1) and (d1), whose top views of soliton profiles are respectively placed in Figure 3(c2) and (d2). One can clearly see the obvious feature of the unstable gap soliton is the appearance of multiple side peaks, while the stable gap soliton is highly localized within a single lattice cell (lattice minimum). In addition to commensurate moiré optical lattices, we have also surveyed the existence of fundamental gap solitons in incommensurate moiré lattice with non-Pythagorean angle θ=π/4, under which the width of first finite gap is very finite, as displayed by the associated dependency P(b) in Figure 3(b). Because of a much larger primitive lattice cell for incommensurate moiré lattice (approximated by an effective Pythagorean lattice but with an enormous Pythagorean triple (a, b, c)), the gap solitons should be prepared on position of the lattice minimum (which is wide too), so that the corresponding soliton power P grows sharply compared to that with a smaller periodicity (periodic moiré lattice), this case is in contrast difference to the fundamental soliton (but not a gap soliton) formation in the semi-infinite gap (formed by total internal reflections) of the incommensurate photonic moiré lattices [17]. This can be explained by the power threshold of the excitation of dissipative gap solitons within the finite gaps (formed by Bragg reflections), such power threshold is needed to fight against the strong multiple Bragg scattering inside the gaps. The typical spatial patterns and contour profiles of the fundamental gap solitons in the midst of the first gap and near the gap edge are depicted in Figure 3(e1) and (f1), and Figure 3(e2) and (f2), respectively, showing a complex spatial soliton structure with substantial side peaks.

Figure 3

Solitons power P versus propagation constant b for commensurate (a) and incommensurate (b) moiré optical lattices. Profiles (middle line) and the contour plots (bottom line) of the fundamental gap solitons corresponding, respectively, to the marked points A and B in (a), and C and D in (b) with different b values: (c1) b=-9.92, (d1) b=-7.34, (e1) b=-13.5930, (f1) b=-13.5928.

In the perturbed propagation dynamics, the unstable fundamental dissipative gap soliton would loose its coherence by subtracting its central profile and expanding its side peaks to large and complex shapes which finally destroy the whole waveform, as displayed in the first line of Figure 4. The stable dissipative gap soliton which are excited in the midst of the first gap of the underlying linear Bloch-wave spectrum, by contrast, becomes unchanged for both centrally (central profile) and collectively, according to the bottom line of Figure 4. The last case proves that the moiré optical lattices provide a flexible platform for creating and stabilizing localized gap modes, enabling the research of soliton physics and detailed dynamical processes control (particularly for linear and nonlinear light field manipulation) in two-dimensional synthetic real nonlinear physical systems with configurable geometrical structures.

Figure 4

Perturbed propagation dynamics of unstable (a1–a4) and stable (b1–b4) fundamental gap solitons in case of commensurate periodic moiré optical lattices corresponding to the marked points A and B in Figure 3(a).

Dissipative gap vortices with topological charge s=1

A natural question of nonlinear physical systems is to quest the formation condition and stability mechanism of vortex gap solitons with vorticity (alias winding number or topological charge) s. In periodic settings and alike, such vortex gap solitons could be easily constructed as hollow composite soliton structures separated by phase distribution s×2. For the simplest case with s=1, such 2 phase structure distributes equally in two-dimensional space. In Figure 5(a), we have accumulated the dependencies P(b) for such simplest dissipative gap vortices, with the solid line represents the stability region while the dashed line for unstable region. One can see an obvious feature is that the unstable region extends (the stable region narrows) for dissipative gap vortices compared with their gap solitons counterpart in Figure 3(a). In the middle line of Figure 5, we have displayed the top view of an unstable dissipative vortex gap soliton, its contour plot and the spatial phase structure; the twisting wave structure and the concomitant multiple side peaks are prominent features. Whereas typical spatial configuration of a stable dissipative gap vortex is shown in the bottom line of Figure 5, manifesting a clear picture with clean profile and phase distribution. Broadly, such hollow four-peak vortex structure can be regarded as the arrangement of four fundamental gap solitons entangled by winding number s=1.

Figure 5

(a) Vortex gap solitons power P versus propagation constant b for commensurate moiré optical lattices. Profiles (b1, c1), the contour plots (b2, c2) and phase structures (b3, c3) of the gap vortices (vortex gap solitons) with topological charge s=1, they are corresponding, respectively, to the marked points E and F in (a) with different b values: (b1) b=-9.92 and (c1) b=-7.34.

We further present detailed dynamical propagation evolutions of such hollow four-peak dissipative gap vortices in Figure 6, the top line of which depicts the case of an unstable dissipative vortex gap soliton experiencing a quick expansion in shape (break up the shape-preserving property of soliton); and the stable dissipative vortex gap soliton, by comparison, could keep the shape constant during the long course of propagation, according to the bottom line of Figure 6.

Figure 6

Perturbed propagation dynamics of unstable (a1–a4) and stable (b1–b4) gap vortices in case of commensurate periodic moiré optical lattices corresponding to the marked points E and F in Figure 5(a).

DISCUSSION

Before closing, we would like to stress once again the key subject put forward in this article and to explore the possibility of experimental realization of the predicted results in realistic physical settings. Our subject focused on the excitation and stability of dissipative solitons, which are presently being widely studied in different physical contexts [8, 35, 40-48] while their underlying physics (particularly in periodic potentials [13, 36, 37]) remains largely unknown, in two-dimensional moiré optical lattices which are featured by tunable geometrical structures, extreme band flattening, and unconventional localization-delocalization properties controlled by merely the rotating angle between the constituted sublattices. Although solitons formation and manipulations are being continually revealed in moiré lattices in recent years, these (dissipationless) solitons are only explored in conservative systems [15, 17, 18, 26-33], the formation mechanism and dynamical processes of dissipative solitons in such two-dimensional twisted structures alike remain elusive. Deserved to be mentioned is that the dissipative solitons are grounded on two balanced regimes: the dissipation is balanced by gain, and the nonlinearity neutralizes the dispersion/diffraction, whereas the latter regime dominates the formation of conventional (dissipationless) solitons. Our physical model is in the framework of nonlinear Schrödinger (NLS) equation accounted for the nonlinear light propagation in a defocusing cubic (Kerr) medium with two-photon absorption and linear gain, and transverse shallow refractive index (moiré optical lattice). Such model can be readily realized in nonlinear optics laboratory [23, 50], and can be extended to other scenarios including ultracold atoms.

Our theoretical predictions provide a flexible, easy-to-implement yet powerful platform for uncovering the extraordinary nonlinear properties including solitons’ formation and dynamics and controlling them, for revealing new physics and finding possible applications (including optics communications and light field manipulations and beyond). It consists of two types of dissipative localized gap modes as dissipative gap solitons and vortices supported by the two-dimensional moiré optical lattices with balanced linear gain and nonlinear dissipation, and the finding of wide stability regions within the finite gap of the associated linear Bloch-wave spectra that always present flattened bands, demonstrating that the two-dimensional controllable optical materials with a new degree of freedom, the twisting angle of the constituted sublattices. A natural extension of this work is to consider the two-component model where vector gap modes are worth exploring systematically.

METHOD

Our numerical calculation recipes follow this way: the stationary-soliton solutions of the governing NLS model Eq. (4) are initially sought by means of a powerful and fast-convergent method called modified squared-operator iteration method introduced in Ref. [51]; then the stability and instability regions of the localized gap modes in the midst or at the edges of finite gaps (of the corresponding linear Bloch-wave band structure) are identified via a large number of direct perturbed numerical calculations of the propagation dynamical model (Eq. (1)) through the usage of a highly accurate computational scheme known as fourth-order Runge-Kutta method.

Funding

This work was supported by the National Natural Science Foundation of China (NSFC) (12074423, 11925108, 12301306), the Young Scholar of Chinese Academy of Sciences in western China (XAB2021YN18), the Provisional Science Fund for Distinguished Young Scholars of Shaanxi (2024JC-JCQN-11), and the Beijing Natural Science Foundation (1234039).

Author contributions

L.W. carried out the and numerical calculations and prepared the figures. J.Z. conceived the idea, guided the research and wrote the manuscript. Z. Y and Y. Z co-guided the research and discussions.

Conflict of interest

The authors declare no conflicts of interest.

References

Kivshar YS, Agrawal GP. Optical Solitons: From Fibers to Photonic Crystals. San Diego: Academic Press, 2003 [Google Scholar]
Kartashov YV, Malomed BA, Torner L. Solitons in nonlinear lattices. Rev Mod Phys 2011; 83: 247-305. [Article] [NASA ADS] [CrossRef] [Google Scholar]
Kartashov YV, Astrakharchik GE, Malomed BA, et al. Frontiers in multidimensional self-trapping of nonlinear fields and matter. Nat Rev Phys 2019; 1: 185-197. [Article] [NASA ADS] [CrossRef] [Google Scholar]
Blanco-Redondo A, de Sterke CM, Xu C, et al. The bright prospects of optical solitons after 50 years. Nat Photon 2023; 17: 937-942. [Article] [NASA ADS] [CrossRef] [Google Scholar]
Kartashov YV, Zezyulin DA. Stable multiring and rotating solitons in two-dimensional spin-orbit-coupled Bose-Einstein condensates with a radially periodic potential. Phys Rev Lett 2019; 122: 123201. [Article] [CrossRef] [PubMed] [Google Scholar]
Goblot V, Rauer B, Vicentini F, et al. Nonlinear polariton fluids in a flatband reveal discrete gap solitons. Phys Rev Lett 2019; 123: 113901. [Article] [CrossRef] [PubMed] [Google Scholar]
Zeng L, Zeng J. Gap-type dark localized modes in a Bose-Einstein condensate with optical lattices. Adv Photon 2019; 1: 046004. [CrossRef] [Google Scholar]
Li J, Zeng J. Dark matter-wave gap solitons in dense ultracold atoms trapped by a one-dimensional optical lattice. Phys Rev A 2021; 103: 013320. [Article] [CrossRef] [PubMed] [Google Scholar]
Liu X, Malomed BA, Zeng J. Localized modes in nonlinear fractional systems with deep lattices. Advcd Theor Sims 2022; 5: 2100482. [Article] [Google Scholar]
Chen Z, Zeng J. Nonlinear localized modes in one-dimensional nanoscale dark-state optical lattices. Nanophotonics 2022; 11: 3465-3474. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Li J, Zhang Y, Zeng J. Matter-wave gap solitons and vortices in three-dimensional parity-time-symmetric optical lattices. Science 2022; 25: 104026. [Article] [Google Scholar]
Li J, Zhang Y, Zeng J. 3D nonlinear localized gap modes in Bose-Einstein condensates trapped by optical lattices and space-periodic nonlinear potentials. Adv Photon Res 2022; 3: 2100288. [Article] [CrossRef] [Google Scholar]
Pernet N, St-Jean P, Solnyshkov DD, et al. Gap solitons in a one-dimensional driven-dissipative topological lattice. Nat Phys 2022; 18: 678-684. [Article] [NASA ADS] [CrossRef] [Google Scholar]
Pan Y, Cohen MI, Segev M. Superluminal k-Gap solitons in nonlinear photonic time crystals. Phys Rev Lett 2023; 130: 233801. [Article] [CrossRef] [PubMed] [Google Scholar]
Huang C, Ye F, Chen X, et al. Localization-delocalization wavepacket transition in Pythagorean aperiodic potentials. Sci Rep 2016; 6: 32546. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Wang P, Zheng Y, Chen X, et al. Localization and delocalization of light in photonic moiré lattices. Nature 2020; 577: 42-46. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Fu Q, Wang P, Huang C, et al. Optical soliton formation controlled by angle twisting in photonic moiré lattices. Nat Photon 2020; 14: 663-668. [Article] [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Wang P, Fu Q, Peng R, et al. Two-dimensional Thouless pumping of light in photonic moiré lattices. Nat Commun 2022; 13: 6738. [Article] [CrossRef] [PubMed] [Google Scholar]
Chen Z, Liu X, Zeng J. Electromagnetically induced moiré optical lattices in a coherent atomic gas. Front Phys 2022; 17: 42508. [Article] [NASA ADS] [CrossRef] [Google Scholar]
Tang H, Du F, Carr S, et al. Modeling the optical properties of twisted bilayer photonic crystals. Light Sci Appl 2021; 10: 157. [Article] [Google Scholar]
Mao XR, Shao ZK, Luan HY, et al. Magic-angle lasers in nanostructured moiré superlattice. Nat Nanotechnol 2021; 16: 1099-1105 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Luan HY, Ouyang YH, Zhao ZW, et al. Reconfigurable moiré nanolaser arrays with phase synchronization. Nature 2023; 624: 282-288. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Meng Z, Wang L, Han W, et al. Atomic Bose-Einstein condensate in twisted-bilayer optical lattices. Nature 2023; 615: 231-236. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Du L, Molas MR, Huang Z, et al. Moiré photonics and optoelectronics. Science 2023; 379: 6639 [Google Scholar]
Qian Q, Wan Z, Duan X. Van der Waals integration of artificial heterostructures and high-order superlattices. Natl Sci Open 20232: 20220034 [CrossRef] [Google Scholar]
Huang C, Dong L, Deng H, et al. Fundamental and vortex gap solitons in quasiperiodic photonic lattices. Opt Lett 2021; 46: 5691-5694. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Kartashov YV, Ye F, Konotop VV, et al. Multifrequency solitons in commensurate-incommensurate photonic Moiré lattices. Phys Rev Lett 2021; 127: 163902. [Article] [CrossRef] [PubMed] [Google Scholar]
Kartashov YV. Light bullets in moiré lattices. Opt Lett 2022, 47: 4528-4531 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Ivanov SK, Konotop VV, Kartashov YV, et al. Vortex solitons in moiré optical lattices. Opt Lett 2023; 48: 3797-3800. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Arkhipova AA, Kartashov YV, Ivanov SK, et al. Observation of linear and nonlinear light localization at the edges of moiré arrays. Phys Rev Lett 2023; 130: 083801. [Article] [CrossRef] [PubMed] [Google Scholar]
Liu X, Zeng J. Gap solitons in parity-time symmetric moiré optical lattices. Photon Res 2023; 11: 196-202. [Article] [CrossRef] [Google Scholar]
Liu X, Zeng J. Matter-wave gap solitons and vortices of dense Bose-Einstein condensates in Moiré optical lattices. Chaos Solitons & Fractals 2023; 174: 113869 [Google Scholar]
Liu X, Zeng J. Two-dimensional localized modes in nonlinear systems with linear nonlocality and moiré lattices. Front Phys 2024; 19: 42201. [Article] [NASA ADS] [CrossRef] [Google Scholar]
Liu X, Zeng J. Two-dimensional localized modes in nonlinear systems with linear nonlocality and moiré lattices. Adv Photon Nexus 2024; 19: 42201 [Google Scholar]
Ultanir EA, Stegeman GI, Michaelis D, et al. Stable dissipative solitons in semiconductor optical amplifiers. Phys Rev Lett 2003; 90: 253903. [Article] [CrossRef] [PubMed] [Google Scholar]
Sakaguchi H, Malomed BA. Gap solitons in Ginzburg-Landau media. Phys Rev E 2008; 77: 056606. [Article] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
Sakaguchi H, Malomed BA. Two-dimensional dissipative gap solitons. Phys Rev E 2009; 80: 026606. [Article] [Google Scholar]
Ye F, Huang C, Kartashov YV, et al. Solitons supported by localized parametric gain. Opt Lett 2013; 38: 480-482 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Huang C, Ye F, Malomed BA, et al. Solitary vortices supported by localized parametric gain. Opt Lett 2013; 38: 2177-2180. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Grelu P, Akhmediev N. Dissipative solitons for mode-locked lasers. Nat Photon 2012; 6: 84-92. [Article] [NASA ADS] [CrossRef] [Google Scholar]
Kippenberg TJ, Gaeta AL, Lipson M, et al. Dissipative Kerr solitons in optical microresonators. Science 2018; 361: eaan8083. [Article] [CrossRef] [PubMed] [Google Scholar]
Bao C, Chang W, Yang C, et al. Observation of coexisting dissipative solitons in a mode-locked fiber laser. Phys Rev Lett 2015; 115: 253903. [Article] [CrossRef] [PubMed] [Google Scholar]
Peng J, Boscolo S, Zhao Z, et al. Breathing dissipative solitons in mode-locked fiber lasers. Sci Adv 2019; 5: eaax1110. [Article] [CrossRef] [PubMed] [Google Scholar]
Cao B, Gao C, Liu K, et al. Spatiotemporal mode-locking and dissipative solitons in multimode fiber lasers. Light Sci Appl 2023; 12: 260. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Zhang J, Peng B, Kim S, et al. Optomechanical dissipative solitons. Nature 2021; 600: 75-80. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Karpov M, Guo H, Kordts A, et al. Raman self-frequency shift of dissipative Kerr solitons in an optical microresonator. Phys Rev Lett 2016; 116: 103902. [Article] [CrossRef] [PubMed] [Google Scholar]
Zhang M, Ding S, Li X, et al. Strong interactions between solitons and background light in Brillouin-Kerr microcombs. Nat Commun 2024; 15: 1661. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Malomed BA. Multidimensional dissipative solitons and solitary vortices. Chaos Solitons & Fractals 2022; 163: 112526 [Google Scholar]
Vakhitov NG, Kolokolov AA. Stationary solutions of the wave equation in a medium with nonlinearity saturation. Radiophys Quantum Electron 1973; 16: 783-789. [Article] [NASA ADS] [CrossRef] [Google Scholar]
Wang K, Seidel M, Nagarajan K, et al. Large optical nonlinearity enhancement under electronic strong coupling. Nat Commun 2021; 12: 1486. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Yang J. Nonlinear Waves in Integrable and Nonintegrable Systems. Philadelphia: SIAM, 2010 [CrossRef] [Google Scholar]

All Figures

Figure 1

The contour structures (first column) of 2D moiré optical lattices and the associated band-gap spectra (second column), photonic density of states (third column), the linear Bloch-wave within one unit cell. Contour geometries of periodic (a1, b1, c1) and aperiodic (d1) moiré optical lattices under different twisted angle: (a1) θ=atan(3/4), (b1) θ=atan(5/12), (c1) θ=atan(8/15), and (d1) θ=π=4. The associated band-gap spectra in the reciprocal lattice momentum space (a2, b2, c2, d2) and the photonic density of states (a3, b3, c3, d3). The first four linear Bloch waves (within a primitive lattice cell) of the moiré optical lattice under θ=atan(8/15). Yellow arrows in (a1, b1, c1) denote the primitive lattice vectors.

In the text

Figure 2

(a) Form-factor χ of the linear eigenmode of a moiré optical lattice with the largest propagation constant versus θ and V₂ at V₁=0.1. Yellow dashed lines present the commensurate (periodic) moiré lattices under some of the Pythagorean angles (from left to right) θ=atan(13/84), atan(5/12), atan(8/15), atan(3/4), atan(20/21), and atan(4/3). Eigenmode profiles $| Φ |$ with the largest propagation constant supported by a incommensurate (aperiodic) moiré lattice under twisted non-Pythagorean angle θ=π/4 and with V₁=0.1 for different V₂ values: V₂₌0.6 (b) and V₂=1.6 (c).

In the text

	Figure 3 Solitons power P versus propagation constant b for commensurate (a) and incommensurate (b) moiré optical lattices. Profiles (middle line) and the contour plots (bottom line) of the fundamental gap solitons corresponding, respectively, to the marked points A and B in (a), and C and D in (b) with different b values: (c1) b=-9.92, (d1) b=-7.34, (e1) b=-13.5930, (f1) b=-13.5928.
In the text

	Figure 4 Perturbed propagation dynamics of unstable (a1–a4) and stable (b1–b4) fundamental gap solitons in case of commensurate periodic moiré optical lattices corresponding to the marked points A and B in Figure 3(a).
In the text

	Figure 5 (a) Vortex gap solitons power P versus propagation constant b for commensurate moiré optical lattices. Profiles (b1, c1), the contour plots (b2, c2) and phase structures (b3, c3) of the gap vortices (vortex gap solitons) with topological charge s=1, they are corresponding, respectively, to the marked points E and F in (a) with different b values: (b1) b=-9.92 and (c1) b=-7.34.
In the text

	Figure 6 Perturbed propagation dynamics of unstable (a1–a4) and stable (b1–b4) gap vortices in case of commensurate periodic moiré optical lattices corresponding to the marked points E and F in Figure 5(a).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.