| Issue |
Natl Sci Open
Volume 1, Number 3, 2022
Special Topic: Novel Optoelectronic Devices
|
|
|---|---|---|
| Article Number | 20220019 | |
| Number of page(s) | 20 | |
| Section | Information Sciences | |
| DOI | https://doi.org/10.1360/nso/20220019 | |
| Published online | 03 August 2022 | |
RESEARCH ARTICLE
Programmable unitary operations for orbital angular momentum encoded states
Department of Electronic Engineering, Tsinghua University, Beijing
100084, China
* Corresponding author (email: x-feng@tsinghua.edu.cn)
Received: 12 February 2022
Revised: 31 March 2022
Accepted: 9 May 2022
We have proposed and demonstrated a scalable and efficient scheme for programmable unitary operations in orbital angular momentum (OAM) domain. Based on matrix decomposition into diagonal and Fourier factors, arbitrary matrix operators can be implemented only by diagonal matrices alternately acting on orbital angular momentum domain and azimuthal angle domain, which are linked by Fourier transform. With numerical simulations, unitary matrices with dimensionality of 3×3 are designed and discussed for OAM domain. Meanwhile, the parallelism of our proposed scheme is also presented with two 3×3 matrices. Furthermore, as an alternative to verify our proposal, proof of principle experiments have been performed on path domain with the same matrix decomposition method, in which an average fidelity of 0.97 is evaluated through 80 experimental results with dimensionality of 3×3.
Key words: unitary transformation / orbital angular momentum / spatial mode / spatial light modulator
© The Author(s) 2022. Published by China Science Publishing & Media Ltd. and EDP Sciences.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
INTRODUCTION
Unitary operators are powerful tools in quantum information processing for both investigating non-classical phenomena and exploring quantum computational resources [1]. Great efforts have been made to apply universal linear operation protocols on high-dimensional optical bases, for extending information capacity and enhancing computing versatility [2–4]. Among them, the orbital angular momentum (OAM) [5] modes provide abundant high-dimensional quantum entanglement resources [6–8], while the spiral phase distributions of OAM states have been employed for quantum imaging [9] and remote sensing [10] techniques.
It has been known that any lossless optical setup can be described by a unitary operator [11]. Thus, generally speaking, the generating [12,13], multiplexing [14–16], sorting [17–19] and manipulating [20,21] OAM modes can be considered certain unitary transformations. Here, we are focused on the arbitrary unitary operator within the OAM-domain. It means that both the input and output states are encoded on a series of optical OAM modes, namely the basis. In our scenario, the weight coefficients of input state would be transformed to those of the output with a unitary operator while the basis keeps. Such a setup or device to perform the unitary operation is quite crucial, since it is the fundamental tool to process the high-dimensional information encoded on OAM modes. However, as analyzed in [21], although there have been great achievements about generating and measuring the OAM modes, how to design an on-demand lossless implementation for an arbitrary unitary operator within OAM-domain has not been well-solved yet. The requirement of closed operation has made it tough to demonstrate unitary operations within OAM-domain, especially with the demand for near-unity success probability at the same time. With the technique of OAM parity sorter [17,18], the four-dimensional Pauli  gate and
gate and  gate have been reported [20]. However, it would be complicated to construct arbitrary unitary operators based on
gate have been reported [20]. However, it would be complicated to construct arbitrary unitary operators based on  gates and
gates and  gates. Recently, with multi-plane light conversion (MPLC) [21,22] method, cyclic and Fourier transformations are reported with dimensionality up to five. Though a broad variety of unitary operations can be performed with MPLC approach, the transformation efficiency would decrease significantly when the number of OAM modes exceeds four according to the reports [21], thus near-unity efficiency has not been achieved for higher dimensionalities. For techniques with spin-orbital coupling [23,24], only two OAM modes can be utilized due to the two-dimensional encoding space of spin angular momentum so that such scheme is limited and not scalable. Thus, to achieve an OAM-encoded unitary operation scheme with universality, scalability, and near-unity success probability simultaneously is still an open question.
gates. Recently, with multi-plane light conversion (MPLC) [21,22] method, cyclic and Fourier transformations are reported with dimensionality up to five. Though a broad variety of unitary operations can be performed with MPLC approach, the transformation efficiency would decrease significantly when the number of OAM modes exceeds four according to the reports [21], thus near-unity efficiency has not been achieved for higher dimensionalities. For techniques with spin-orbital coupling [23,24], only two OAM modes can be utilized due to the two-dimensional encoding space of spin angular momentum so that such scheme is limited and not scalable. Thus, to achieve an OAM-encoded unitary operation scheme with universality, scalability, and near-unity success probability simultaneously is still an open question.
In this work, inspired by the Fourier-diagonal decomposition theorem [25,26] and the demonstration of frequency-domain unitary operation protocols [27,28], we extend this technique to optical encoding basis of OAM domain. A scalable and intrinsic near-lossless scheme for programmable unitary gates based on matrix decomposition [25] is proposed and demonstrated with dimensionality of  . Moreover, the parallelism of our proposed scheme is also presented with two 3×3 matrices. Limited by the experimental conditions, only numerical simulations are presented for arbitrary OAM-encoded unitary matrices. It should be mentioned that our proposed scheme could also be applied on other two photonic encoding bases that belong to a Fourier transform pair. Thus, as an alternative to verify our proposal, proof of principle experiments have been performed on path domain, in which average fidelity value of
. Moreover, the parallelism of our proposed scheme is also presented with two 3×3 matrices. Limited by the experimental conditions, only numerical simulations are presented for arbitrary OAM-encoded unitary matrices. It should be mentioned that our proposed scheme could also be applied on other two photonic encoding bases that belong to a Fourier transform pair. Thus, as an alternative to verify our proposal, proof of principle experiments have been performed on path domain, in which average fidelity value of  and transformation efficiency of
and transformation efficiency of  are evaluated through 80 experimental results with matrix dimensionality of
are evaluated through 80 experimental results with matrix dimensionality of .
.
THEORY
Without loss of generality, our target is to implement an arbitrary unitary gate  acting on optical states, which could be expressed as
acting on optical states, which could be expressed as
where  and
and  denote the input and output states. Usually
denote the input and output states. Usually  and
and  are encoded on a series of optical modes, namely the basis, which could be any degree of freedom, including optical path, frequency, temporal-mode, and transverse-spatial-mode. It should be mentioned that here, the bases of both input and output states are considered the same. Thus, with a unitary operator of
are encoded on a series of optical modes, namely the basis, which could be any degree of freedom, including optical path, frequency, temporal-mode, and transverse-spatial-mode. It should be mentioned that here, the bases of both input and output states are considered the same. Thus, with a unitary operator of  , the weight coefficients of
, the weight coefficients of  would be transformed to those of
would be transformed to those of  while the basis is not changed. For most practical applications,
while the basis is not changed. For most practical applications,  is a finite-dimensional operator and can be mathematically expressed as a unitary matrix with respect to the utilized encoding basis. It has been presented [25] that an arbitrary matrix of dimensionality
is a finite-dimensional operator and can be mathematically expressed as a unitary matrix with respect to the utilized encoding basis. It has been presented [25] that an arbitrary matrix of dimensionality  can be mathematically decomposed into the production of diagonal matrices and cyclic matrices alternately, where the total number of matrices is M, or equivalently saying,
can be mathematically decomposed into the production of diagonal matrices and cyclic matrices alternately, where the total number of matrices is M, or equivalently saying,  diagonal matrices
diagonal matrices  spaced by discrete Fourier transformation (DFT) matrix
spaced by discrete Fourier transformation (DFT) matrix  and its inverse matrix, which is also its Hermitian conjugate
and its inverse matrix, which is also its Hermitian conjugate  :
:
where  [26] denotes the number of diagonal matrices required for the decomposition and the actual value would vary according to the target matrices. Specifically, to establish a unitary operator
[26] denotes the number of diagonal matrices required for the decomposition and the actual value would vary according to the target matrices. Specifically, to establish a unitary operator  , the diagonal matrices
, the diagonal matrices  in eq. (2) would also be unitary. To clearly present our idea, the right-hand term in the first line of eq. (2) is modified as the form of the second one. Particularly, the terms in brackets are diagonal matrices sandwiched by DFT and inverse DFT matrices. Actually, they are also diagonal matrices but acting on a transformed domain, which is determined by the DFT. Thus, eq. (2) could be understood as that a unitary operator can be decomposed into a series of diagonal matrices in two domains, which are linked with Fourier transformation. A diagonal matrix, which is also referred to as a spectral shaper, would not lead to cross-mode effects. Actually, the required cross-components for unitary operations are achieved by DFT matrices in eq. (2). Thus, if two photonic degree-of-freedoms (DOFs) are Fourier transform pair, any unitary matrix can be implemented by performing diagonal matrix operations on these two DOFs in succession for the investigated photonic qudits.
in eq. (2) would also be unitary. To clearly present our idea, the right-hand term in the first line of eq. (2) is modified as the form of the second one. Particularly, the terms in brackets are diagonal matrices sandwiched by DFT and inverse DFT matrices. Actually, they are also diagonal matrices but acting on a transformed domain, which is determined by the DFT. Thus, eq. (2) could be understood as that a unitary operator can be decomposed into a series of diagonal matrices in two domains, which are linked with Fourier transformation. A diagonal matrix, which is also referred to as a spectral shaper, would not lead to cross-mode effects. Actually, the required cross-components for unitary operations are achieved by DFT matrices in eq. (2). Thus, if two photonic degree-of-freedoms (DOFs) are Fourier transform pair, any unitary matrix can be implemented by performing diagonal matrix operations on these two DOFs in succession for the investigated photonic qudits.
It should be mentioned that for the Fourier terms in eq. (2), it is not required to actually construct the corresponding matrix operation. These Fourier and inverse Fourier operators are naturally inserted in eq. (2) when the spectral shaping is alternatively performed on two DOFs linked by Fourier transform. Actually, there are some Fourier transform pairs, which have been well investigated in photonic domain, including linear basis (x-basis) and transverse wave vector basis (k-basis) [29,30], OAM and azimuthal angle [31], and frequency and time-bin. Specifically, arbitrary unitary operators with OAM encoded states can be implemented with diagonal matrices in the OAM and azimuthal angle domain.
With well-defined OAM basis, an arbitrary state vector  can be expanded as
can be expanded as
where  represent OAM spectrum coefficients and
represent OAM spectrum coefficients and  denotes the
denotes the  eigenstate with OAM of
eigenstate with OAM of  carried per photon. As mentioned above, in our scenario, the spectrum coefficients of
carried per photon. As mentioned above, in our scenario, the spectrum coefficients of 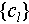 would be transformed with a unitary operator of U while the basis of
would be transformed with a unitary operator of U while the basis of  keeps. To perform the decomposition of eq. (2), both the OAM domain and corresponding Fourier transformation should be employed. It has been investigated that transverse OAM basis
keeps. To perform the decomposition of eq. (2), both the OAM domain and corresponding Fourier transformation should be employed. It has been investigated that transverse OAM basis  and angle basis
and angle basis  are connected via Fourier transformation [31]:
are connected via Fourier transformation [31]:
Thus, it is feasible to implement well-designed diagonal matrices within the OAM-domain and angle-domain alternately to achieve any target OAM-domain matrix operator with decomposition form shown in eq. (2). The question is how to implement the diagonal matrices for both OAM and angle domains. Figure 1 shows an example of OAM-domain unitary operator with the three-layer scheme corresponding to the case of  in eq. (2). There are two layers to implement diagonal matrices in angle domain and one layer for OAM domain. As shown later, this scheme could perform most unitary operations with dimensionality of
in eq. (2). There are two layers to implement diagonal matrices in angle domain and one layer for OAM domain. As shown later, this scheme could perform most unitary operations with dimensionality of  , and some particular operations of
, and some particular operations of  and
and  .
.
 |
Figure 1 The scheme of OAM-domain unitary operation with three-layer. |
In the angle-domain, a diagonal matrix can be readily achieved by a single wave front modulation element such as a spatial light modulator (SLM) [32] or metasurfaces [33]. Here, the SLM is considered and noted as angle modulator in Figure 1. A typical angle modulation function  can be achieved by the pattern
can be achieved by the pattern  settled on SLM:
settled on SLM:
where  and
and  indicate the radius and azimuthal angle under polar coordinates in the transverse plane according to beam propagation direction, respectively. Thus, the only question is how to realize the required diagonal matrices in OAM-domain, which is also referred to as an OAM spectral shaper [34].
indicate the radius and azimuthal angle under polar coordinates in the transverse plane according to beam propagation direction, respectively. Thus, the only question is how to realize the required diagonal matrices in OAM-domain, which is also referred to as an OAM spectral shaper [34].
Here, a straight-forward method is considered to achieve a programmable and arbitrary OAM spectral shaper. With the help of OAM mode-sorter based on Cartesian to log-polar coordinate transformation [35], each OAM eigenstate can be mapped to different position in the focal plane. As shown in Figure 1, two static optical elements  and
and  are employed to perform the mode sorter [35,36]:
are employed to perform the mode sorter [35,36]:
where  and
and  are adjustable parameters, which can be designed according to the beam width of the exact transverse optical field. After passing through these two static optical elements together with an auxiliary lens of focal length
are adjustable parameters, which can be designed according to the beam width of the exact transverse optical field. After passing through these two static optical elements together with an auxiliary lens of focal length  , the
, the  OAM eigenstate is sorted to a single spot, in which the center coordinate
OAM eigenstate is sorted to a single spot, in which the center coordinate  in the focal plane reads,
in the focal plane reads,
while the center coordinate  is only determined by parameter
is only determined by parameter  in eq. (6) and irrelevant to
in eq. (6) and irrelevant to  . According to eq. (7), different OAM modes are spatially separated in the focal plane of the auxiliary lens after the mode sorter consists of
. According to eq. (7), different OAM modes are spatially separated in the focal plane of the auxiliary lens after the mode sorter consists of  and
and  shown in eq. (6). The coordinate
shown in eq. (6). The coordinate  of the focus center of the
of the focus center of the  OAM mode is proportional to the value of
OAM mode is proportional to the value of  . As is shown in Figure 1, an SLM is employed and spatially divided into several blocks along the
. As is shown in Figure 1, an SLM is employed and spatially divided into several blocks along the  -axis, which are aligned with the coordinates of the focus centers of each OAM mode. Different phase modulations are settled on these blocks to achieve spectral shaping on OAM modes. In practical implementations, the OAM spectral shaper is determined by the target unitary matrix of U. Suppose that the desired spectral shaping function is noted as
-axis, which are aligned with the coordinates of the focus centers of each OAM mode. Different phase modulations are settled on these blocks to achieve spectral shaping on OAM modes. In practical implementations, the OAM spectral shaper is determined by the target unitary matrix of U. Suppose that the desired spectral shaping function is noted as  , the OAM spectral shaper can be implemented with the following wave front modulation function:
, the OAM spectral shaper can be implemented with the following wave front modulation function:
where  rounds the value to the nearest integer. As indicated in Figure 1, such shape function of
rounds the value to the nearest integer. As indicated in Figure 1, such shape function of  is achieved with another SLM, which is placed at the focal plane of the auxiliary lens after the second optical element of
is achieved with another SLM, which is placed at the focal plane of the auxiliary lens after the second optical element of  . After OAM spectral shaping, another two static optical elements are required to recover the OAM modes, i.e., to transform the Cartesian coordinate back to log-polar coordinate. The mode-sorter has been proved to be reversible [37] and the static optical elements to perform the reverse mode-sorting are exactly the same as those shown in eq. (6). Since the static elements for OAM mode-sorter can be replaced by customized spherical lens and cylindrical lens [36], only one programmable SLM performing
. After OAM spectral shaping, another two static optical elements are required to recover the OAM modes, i.e., to transform the Cartesian coordinate back to log-polar coordinate. The mode-sorter has been proved to be reversible [37] and the static optical elements to perform the reverse mode-sorting are exactly the same as those shown in eq. (6). Since the static elements for OAM mode-sorter can be replaced by customized spherical lens and cylindrical lens [36], only one programmable SLM performing 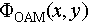 shown in eq. (8) would be enough for any OAM spectral shaping task.
shown in eq. (8) would be enough for any OAM spectral shaping task.
SIMULATION
We have mathematically modeled the scheme shown in Figure 1 and simulated the field evolution according to Huygens-Fresnel principle under paraxial approximation. According to the parameters of SLMs (Holoeye Pluto), the simulation area is set to  pixels with a pixel size of
pixels with a pixel size of  . The operation wavelength is considered 1550 nm.
. The operation wavelength is considered 1550 nm.
Firstly, the performance of our proposed OAM spectral shaper is evaluated. As shown in Figure 2A, L1 and L2 are lenses with focal length of  . A superposed state with 11 OAM modes is shown in Figure 2C as the input state. The mode interval between adjacent OAM encoding channels is chosen as 4 to compress the mode crossing induced by mode-sorter [38]. From left to right, Figure 2B shows field evolution of an initial superposed OAM state passing through the spectral shaper step-by-step (from index 1 to index 6), while the corresponding positions are marked in Figure 2A. Here, brightness and color indicate the amplitude and phase distributions, respectively. After the OAM mode-sorter, the initial angular momentum state is mapped to linear state. With the help of lens L1, linear momentum is transformed to linear coordinate in the focal plane. Then the OAM spectral shaping is performed by the SLM settled on the focal plane. After that, the optical vortex is rolled back again by another reversely operating mode-sorter.
. A superposed state with 11 OAM modes is shown in Figure 2C as the input state. The mode interval between adjacent OAM encoding channels is chosen as 4 to compress the mode crossing induced by mode-sorter [38]. From left to right, Figure 2B shows field evolution of an initial superposed OAM state passing through the spectral shaper step-by-step (from index 1 to index 6), while the corresponding positions are marked in Figure 2A. Here, brightness and color indicate the amplitude and phase distributions, respectively. After the OAM mode-sorter, the initial angular momentum state is mapped to linear state. With the help of lens L1, linear momentum is transformed to linear coordinate in the focal plane. Then the OAM spectral shaping is performed by the SLM settled on the focal plane. After that, the optical vortex is rolled back again by another reversely operating mode-sorter.
 |
Figure 2 Simulations of OAM spectral shaper with Huygens-Fresnel principle. (A) The scheme of OAM spectral shaper. (B) Step-by-step field evolution of an initial superposed OAM state passing through the spectral shaper. (C) Initial OAM spectrum. (D) Output OAM spectrum. The brightness and color indicate the amplitude and phase distributions, respectively. |
The OAM spectral shaper under test is expressed as  . Since only lossless scheme and unitary matrices are concerned, the required diagonal operators in matrix decomposition in eq. (2) are phase-only and thus referred to as
. Since only lossless scheme and unitary matrices are concerned, the required diagonal operators in matrix decomposition in eq. (2) are phase-only and thus referred to as  for simplicity. In the following sections,
for simplicity. In the following sections,  and
and  are adopted instead of
are adopted instead of and
and  for angular phase modulation and OAM phase spectral shaping, respectively.
for angular phase modulation and OAM phase spectral shaping, respectively.
In the case shown in Figure 2,  means
means  and
and  phase modulation for adjacent OAM channels. Actually, it is the most challenging case since modulation function is “sharpest” as well as the phase crosstalk is maximum. Such extreme example is considered to examine the crosstalk tolerance of our proposed OAM spectral shaper. Besides,
phase modulation for adjacent OAM channels. Actually, it is the most challenging case since modulation function is “sharpest” as well as the phase crosstalk is maximum. Such extreme example is considered to examine the crosstalk tolerance of our proposed OAM spectral shaper. Besides,  is a typical clock matrix and could also be achieved by field rotation of
is a typical clock matrix and could also be achieved by field rotation of  rad with a Dove prism [39]. Thus, the OAM spectral shaping effect can be observed intuitively through the rotation between the output and initial field in Figure 2B. We also provided the OAM spectrum after spectral shaper in Figure 2D. The complex OAM spectrum is calculated with mode-matching method [40]. With this method, the eigenmode expansions of the input and output OAM states during simulation can be evaluated and are expressed as
rad with a Dove prism [39]. Thus, the OAM spectral shaping effect can be observed intuitively through the rotation between the output and initial field in Figure 2B. We also provided the OAM spectrum after spectral shaper in Figure 2D. The complex OAM spectrum is calculated with mode-matching method [40]. With this method, the eigenmode expansions of the input and output OAM states during simulation can be evaluated and are expressed as  and
and  , where
, where  and
and  are input and output OAM spectrum coefficients, respectively. Thus, the spectral shaping function
are input and output OAM spectrum coefficients, respectively. Thus, the spectral shaping function  can be deduced with
can be deduced with  . From these simulations, the fidelity value of output OAM spectrum compared with the target one is 0.988, which is estimated according to eq. (9). It can be seen that the OAM spectral shaper is valid for high-dimensional input states and the unitary operations could be achieved in succession.
. From these simulations, the fidelity value of output OAM spectrum compared with the target one is 0.988, which is estimated according to eq. (9). It can be seen that the OAM spectral shaper is valid for high-dimensional input states and the unitary operations could be achieved in succession.
Secondly, the OAM spectral shaping function  and two required angular modulation functions of
and two required angular modulation functions of 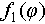 and
and  for a given target matrix are calculated through an optimization algorithm [20]. Our target is to achieve the maximum success probability. The success probability is proportional to the trace value of
for a given target matrix are calculated through an optimization algorithm [20]. Our target is to achieve the maximum success probability. The success probability is proportional to the trace value of  subject to
subject to  , where
, where  and
and  denote target unitary matrix and designed matrix, respectively. The success probability of implemented matrix after optimization is calculated by
denote target unitary matrix and designed matrix, respectively. The success probability of implemented matrix after optimization is calculated by  . The fidelity is defined as [41]
. The fidelity is defined as [41]
The designed matrix  in eq. (9) is calculated by OAM spectral shaping function
in eq. (9) is calculated by OAM spectral shaping function  and two angular modulation functions
and two angular modulation functions  and
and  . Here, we give an example with dimensionality of
. Here, we give an example with dimensionality of  :
:
The number  in eq. (10) is the dimensionality of numerical optimization. The central
in eq. (10) is the dimensionality of numerical optimization. The central  region in the left side of eq. (10) is the optimized matrix
region in the left side of eq. (10) is the optimized matrix  . We note that
. We note that  , where
, where  is the dimensionality of target matrix (
is the dimensionality of target matrix ( for the case in eq. (10)) and
for the case in eq. (10)) and  is the number of guard bands. The guard bands are required to eliminate cut-off effects, which arises from the differences between the finite-dimension discrete Fourier transform required in eq. (2) and the infinite-dimension nature of the Fourier relation of OAM eigenstates and angle eigenstates expressed in eq. (4). In this work, both for the OAM-encoding and path-encoding, the number
is the number of guard bands. The guard bands are required to eliminate cut-off effects, which arises from the differences between the finite-dimension discrete Fourier transform required in eq. (2) and the infinite-dimension nature of the Fourier relation of OAM eigenstates and angle eigenstates expressed in eq. (4). In this work, both for the OAM-encoding and path-encoding, the number  is chosen to be
is chosen to be  during the numerical calculation of spectral shaping functions. The DFT matrices in eq. (10) are normalized with
during the numerical calculation of spectral shaping functions. The DFT matrices in eq. (10) are normalized with  in amplitude so that
in amplitude so that  Besides, we have
Besides, we have  if and only if all other elements that share the same rows or columns with the central
if and only if all other elements that share the same rows or columns with the central  block are zero.
block are zero.
The angular modulation functions  and
and  are quasi-continuous since the
are quasi-continuous since the  interval is divided into
interval is divided into 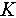 bins. The angular modulation functions are represented by sine expansion:
bins. The angular modulation functions are represented by sine expansion:
The parameters  and
and are to be determined. The scalar
are to be determined. The scalar  may grow as the size
may grow as the size  of target matrices increases, to ensure enough interactions between farther OAM channels. Here
of target matrices increases, to ensure enough interactions between farther OAM channels. Here  and
and  are chosen for 2-dimensional and 3-dimensional unitary matrices, respectively. By choosing finite series expansion of sine expression, a relatively smooth modulation function can be obtained. Thus, the corresponding phase masks could have lower spatial resolution according to the Nyquist criterion and can be realized with more facility. The number
are chosen for 2-dimensional and 3-dimensional unitary matrices, respectively. By choosing finite series expansion of sine expression, a relatively smooth modulation function can be obtained. Thus, the corresponding phase masks could have lower spatial resolution according to the Nyquist criterion and can be realized with more facility. The number  in eq. (11) is determined by the dimension
in eq. (11) is determined by the dimension  of target matrix since higher orders of sine components in angular modulation functions allow interactions between farther OAM eigenstates.
of target matrix since higher orders of sine components in angular modulation functions allow interactions between farther OAM eigenstates.  is chosen in our simulations. The entire optimization is done with the MATLAB “fmincon” function. To further explain the optimization procedure and provide an executable example, the functions
is chosen in our simulations. The entire optimization is done with the MATLAB “fmincon” function. To further explain the optimization procedure and provide an executable example, the functions  ,
,  and
and  required for
required for  and
and  Hadamard matrices
Hadamard matrices  and
and  as well as modulation functions settled on SLMs are shown in Figure 3.
as well as modulation functions settled on SLMs are shown in Figure 3.
 |
Figure 3 Optimized approach for OAM-domain Hadamard matrices with dimensionality of |
The schematic setup for OAM-domain matrix transformation is shown in Figure 3A. Three SLMs labelled as SLM1, SLM2, and SLM3 perform the first angular modulator, OAM spectral shaper, and the second angular modulator, respectively. The colored phase modulation patterns corresponding to each SLM are also shown. For Hadamard matrix  , the optimized angular modulation functions are shown under polar coordinates in Figure 3B, where the red and blue solid lines indicate
, the optimized angular modulation functions are shown under polar coordinates in Figure 3B, where the red and blue solid lines indicate  and
and  , respectively. The unit of polar axis in Figure 3B is rad. The optimized OAM spectral shaper noted as
, respectively. The unit of polar axis in Figure 3B is rad. The optimized OAM spectral shaper noted as  is shown in Figure 3C, where the OAM eigenstates of
is shown in Figure 3C, where the OAM eigenstates of  and
and  are chosen as encoding channels for
are chosen as encoding channels for  . In Figure 3C, 10 guard bands are plotted. Since the optimized spectral shaping functions tend to converge for more guard bands, much less OAM channels need to be modulated even when number
. In Figure 3C, 10 guard bands are plotted. Since the optimized spectral shaping functions tend to converge for more guard bands, much less OAM channels need to be modulated even when number  in eq. (10) is chosen to be as large as 64.
in eq. (10) is chosen to be as large as 64.
Numerical estimation is made to quantize the influence of the number of guard bands on transformation fidelity and success probability. For those encoding channels beyond guard bands, there are two situations that have to be considered. The signals that enter those channels are left unchanged for OAM-encoding since those OAM channels always exist objectively. For path-encoding employed in experiments in section 4, the channels beyond guard bands are filtered out since the number of accessible encoding channels is determined by the size of SLMs (Experiment). For both cases, the fidelity and probability of unitary transformation as functions of numbers of guard bands are plotted in Figure 4. The target matrices are chosen as  and
and  in Figures 4A and 4B and Figures 4C and 4D, respectively.
in Figures 4A and 4B and Figures 4C and 4D, respectively.
 |
Figure 4 Fidelity and probability of unitary transformation as functions of numbers of guard bands. The target matrices are chosen as |
According to the numerical results shown in Figure 4, the condition of  would be enough for most practical cases. Thus, only two or three guard bands are required for practical
would be enough for most practical cases. Thus, only two or three guard bands are required for practical  gate. Due to the value of
gate. Due to the value of  , the optimized angular modulation function shown in Figure 3B seems quasi-continuous. Those optimization results for Hadamard matrix
, the optimized angular modulation function shown in Figure 3B seems quasi-continuous. Those optimization results for Hadamard matrix  are shown in Figures 3D and 3E, where OAM eigenstates
are shown in Figures 3D and 3E, where OAM eigenstates  ,
,  and
and  are chosen as encoding channels. According to the optimization, the fidelity above 0.999 and success probability above 0.970 are achieved simultaneously for
are chosen as encoding channels. According to the optimization, the fidelity above 0.999 and success probability above 0.970 are achieved simultaneously for 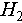 and
and 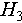 . After the phase patterns settled on SLMs are obtained, the field evolution of Hadamard matrix
. After the phase patterns settled on SLMs are obtained, the field evolution of Hadamard matrix  has been calculated according to Huygens-Fresnel principle. The OAM eigenstates of
has been calculated according to Huygens-Fresnel principle. The OAM eigenstates of  and
and 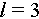 are chosen to be the encoding channels. The transformation fidelity is calculated as 0.998.
are chosen to be the encoding channels. The transformation fidelity is calculated as 0.998.
In Figure 5, each row represents the field evolution of different initial OAM states and six columns are corresponding to the initial field, field after SLM1, field after mode-sorter, field before SLM2, field before L2, and output field (from left to right). All rows are achieved with the same angular phase patterns so that the same OAM phase spectral modulation functions are obtained. Moreover, in each map, the brightness and color are corresponding to the amplitude and phase, respectively. It should be mentioned that there is no need for post-selection to perform OAM-domain closed transformation with our proposal and thus the near-unity success probability is preserved. Thus, our results for implementing OAM-domain Hadamard matrix (or OAM beam splitter) may inspire some new applications such as observation of OAM-domain Hong-Ou-Mandel (HOM) effect [42] and OAM-encoded measurement-device-independent quantum key distribution (MDI-QKD) [43].
 |
Figure 5 Step-by-step field evolution of OAM-domain Hadamard matrix. |
Additionally, another important feature of our proposal is parallel computing, which is considered an advantage of optical information processing. With our scheme, the same matrix could be applied on different OAM channels simultaneously without any extra hardware cost. To further explain this, the optimized OAM spectral shaping function  is shown in Figure 6A for two
is shown in Figure 6A for two  gates acting on two groups of OAM channels with
gates acting on two groups of OAM channels with  and
and  . For SLM modulation functions, the only change is to replace the OAM spectral shaping function
. For SLM modulation functions, the only change is to replace the OAM spectral shaping function  by
by
 (13)
where
(13)
where  denotes convolution and
denotes convolution and  denotes the Dirac delta function. The OAM charge
denotes the Dirac delta function. The OAM charge  is the central OAM channels utilized by each identical matrix. It is unnecessary to change the angular modulation functions
is the central OAM channels utilized by each identical matrix. It is unnecessary to change the angular modulation functions  and
and  for such parallel processing. Two
for such parallel processing. Two  gates acting on OAM channels with
gates acting on OAM channels with  and
and  are simulated and the entire
are simulated and the entire  matrix operator is evaluated and shown in Figure 6B. Furthermore, the simulated results of dual
matrix operator is evaluated and shown in Figure 6B. Furthermore, the simulated results of dual  gates are shown in Figure 6C. The utilized OAM channels are
gates are shown in Figure 6C. The utilized OAM channels are  and
and  . The
. The  gate is also noted as
gate is also noted as  DFT. In Figure 6C, the
DFT. In Figure 6C, the  gate is tested with input superposed OAM states of
gate is tested with input superposed OAM states of  and
and  one-by-one, while
one-by-one, while  denotes the nth column of
denotes the nth column of  . With this test, the phase accuracy of the unitary matrix can be evaluated. The colored bars and empty bars in Figure 6C indicate input complex OAM spectrum and output OAM spectrum, respectively. It should be mentioned that the simulation in Figure 6 is made under the same three-layer model as shown in Figure 3A. It has been observed that the OAM-domain parallel gates work well without any extra hardware cost.
. With this test, the phase accuracy of the unitary matrix can be evaluated. The colored bars and empty bars in Figure 6C indicate input complex OAM spectrum and output OAM spectrum, respectively. It should be mentioned that the simulation in Figure 6 is made under the same three-layer model as shown in Figure 3A. It has been observed that the OAM-domain parallel gates work well without any extra hardware cost.
 |
Figure 6 The OAM-domain parallel |
In Figures 6D and 6E, the performances of parallel  and
and  gates are plotted as functions of OAM modes separation, respectively. It could be found that the parallel gates operate independently with negligible crosstalk if the interval of utilized OAM channels is larger than two times of the number of necessary guard bands.
gates are plotted as functions of OAM modes separation, respectively. It could be found that the parallel gates operate independently with negligible crosstalk if the interval of utilized OAM channels is larger than two times of the number of necessary guard bands.
Actually, the number of parallel matrices is only limited by the number of available OAM channels. Here, the mode interval of adjacent OAM channels is settled as 4 to avoid mode crosstalk induced by OAM mode-sorters. The OAM channel resources would be utilized more efficiently if some efforts are made to reduce the crosstalk [44]. According to the mathematic decomposition form in eq. (2) as well as the numerical optimization form in eq. (10), it is quite straight forward to extend this three-layer structure in Figure 1 to larger scales. With alternately cascaded angular spectral shaper layers and OAM spectral shaper layers, the system arrangement would grow with complexity of  [26] according to the dimensionality
[26] according to the dimensionality  of the target unitary matrix.
of the target unitary matrix.
In our design, the free space focus systems shown in the conceptual setup in Figure 3A only serve for the OAM mode-sorters. Besides this, there is no need for free-space propagation or extra Fourier transformation blocks between two adjacent layers of spectral shapers. For OAM domain unitary operations, this is one of the main differences to the MPLC method [21,22], in which some free-space propagation between adjacent layers is required. It should be mentioned that our proposal is not constrained by the actual method of OAM spectral shaping. In our simulation, the OAM spectral shaping is achieved with OAM mode-sorters, which would induce extra experimental difficulties. Actually, the system arrangement shown in Figure 1 could be largely simplified with compact OAM spectral shaper. For some specific target matrices, the recently reported single-step OAM shaper [34,45] may be employed.
EXPERIMENT
Due to the lack of OAM mode-sorter elements, which requires advanced 3D printing technology, proof-of-principle experiments in path domain are performed to verify our proposed scheme. To utilize the matrix decomposition in eq. (2), we notice that there is a one-to-one mapping from transverse wave vector in the object plane to transverse coordinate in the focal plane. To encode qudits, the path basis can be defined by a series of transverse coordinates lying on y-axis in the focal plane. Thus, the optical field  in the object plane is linked to the aforementioned path-encoded state vector through the Fourier transformation and expressed as
in the object plane is linked to the aforementioned path-encoded state vector through the Fourier transformation and expressed as
where  denotes the complex amplitude of the nth path-encoding channel in the focal plane. It should be mentioned that
denotes the complex amplitude of the nth path-encoding channel in the focal plane. It should be mentioned that  and the path-encoded state vector of
and the path-encoded state vector of  are equivalent expressions of the same state under momentum space and position space, respectively. Therefore, unitary operations can be achieved by alternately performing spectral shaping in momentum space and position space. The distance between adjacent paths is noted as
are equivalent expressions of the same state under momentum space and position space, respectively. Therefore, unitary operations can be achieved by alternately performing spectral shaping in momentum space and position space. The distance between adjacent paths is noted as  , while the distance between adjacent SLMs is set to
, while the distance between adjacent SLMs is set to  . This leads to a corresponding transverse wave vector of
. This leads to a corresponding transverse wave vector of
 |
Figure 7 (A) Conceptual set-up of path-encoded matrix transformation, and the modulation functions settled on SLMs. (B) Optimized phase modulation function settled on SLM2 for implementing |
The conceptual setup is shown in Figure 7A. The modulation functions on SLM1 and SLM3 are settled as the following to introduce the required transverse wave vector components:
 (16)
Eq. (16) is very similar to the azimuthal phase modulation function in eq. (11) for OAM-domain matrix transformation. The parameters
(16)
Eq. (16) is very similar to the azimuthal phase modulation function in eq. (11) for OAM-domain matrix transformation. The parameters  and
and  are to be determined by optimizations and possess the same meanings as shown in eq. (11). The only difference is that the azimuthal coordinate
are to be determined by optimizations and possess the same meanings as shown in eq. (11). The only difference is that the azimuthal coordinate  is replaced by linear coordinate
is replaced by linear coordinate  . The modulation function on SLM2 is settled as
. The modulation function on SLM2 is settled as
 (17) which is also a direct mapping of eq. (8). The function of
(17) which is also a direct mapping of eq. (8). The function of  represents the phase modulation applied to the nth path channel. Practically,
represents the phase modulation applied to the nth path channel. Practically,  ,
,  ,
,  are optimized with the same method as
are optimized with the same method as  ,
,  ,
,  in OAM-domain unitary transformation. The
in OAM-domain unitary transformation. The  gate is shown as an example to clarify it. The optimized
gate is shown as an example to clarify it. The optimized  is shown in Figure 7B, where path channels
is shown in Figure 7B, where path channels  are chosen for encoding. The
are chosen for encoding. The  and
and  functions are shown in Figure 7C as phase-only gratings programmed on SLM1 and SLM3, respectively. Gratings can be considered spectral shaping in transverse momentum space. Here, only one period of grating is plotted for simplicity and clarity. A lens with focal length of
functions are shown in Figure 7C as phase-only gratings programmed on SLM1 and SLM3, respectively. Gratings can be considered spectral shaping in transverse momentum space. Here, only one period of grating is plotted for simplicity and clarity. A lens with focal length of  is added on SLM2 to maintain the Fourier relation between optical fields on adjacent SLM planes. It should be mentioned that the one-dimensional Fourier relation is employed here, which can be expressed as a Fourier transform matrix and is different from the two-dimensional Fourier transform that is achieved by free space propagation. Two extra lenses noted as L1 and L2 in Figure 7A are employed to compensate for transverse wave vector so that the setup can be scalable. As indicated in eq. (14), we are only interested in the field variations along y-axis in the transverse plane. The field along x-axis is simply set as Gaussian shape and some ancillary lenses are programmed on SLMs to compensate the natural expansion of Gaussian beams.
is added on SLM2 to maintain the Fourier relation between optical fields on adjacent SLM planes. It should be mentioned that the one-dimensional Fourier relation is employed here, which can be expressed as a Fourier transform matrix and is different from the two-dimensional Fourier transform that is achieved by free space propagation. Two extra lenses noted as L1 and L2 in Figure 7A are employed to compensate for transverse wave vector so that the setup can be scalable. As indicated in eq. (14), we are only interested in the field variations along y-axis in the transverse plane. The field along x-axis is simply set as Gaussian shape and some ancillary lenses are programmed on SLMs to compensate the natural expansion of Gaussian beams.
Eighty different unitary transformations have been performed with the experimental setup as shown in Figure 8, while 75 of them are randomly generated. For each different target matrix, a particular set of modulation functions has to be optimized. The number of guard bands is set as  . As shown in Figure 8, a laser beam of zero-order Gaussian profile operating at 1550 nm (RIO Orion) is incident to the optical system through a collimator. Three SLMs (Holoeye Pluto) operating with reflective mode are utilized and the focal length
. As shown in Figure 8, a laser beam of zero-order Gaussian profile operating at 1550 nm (RIO Orion) is incident to the optical system through a collimator. Three SLMs (Holoeye Pluto) operating with reflective mode are utilized and the focal length  mentioned before is set as 40 cm. The distance
mentioned before is set as 40 cm. The distance  between adjacent paths is designed as 2 mm considering the reflective area of SLMs. Specially, the input state is both generated and switched by SLM1. The transverse k-space expression
between adjacent paths is designed as 2 mm considering the reflective area of SLMs. Specially, the input state is both generated and switched by SLM1. The transverse k-space expression  in eq. (14) of the input state, or equivalently saying, the interference pattern of the input beams at SLM1 plane in conceptual setup in Figure 7A is pre-calculated and directly settled on SLM1 to modulate the incident Gaussian beam from the collimator in experimental setup shown in Figure 8.
in eq. (14) of the input state, or equivalently saying, the interference pattern of the input beams at SLM1 plane in conceptual setup in Figure 7A is pre-calculated and directly settled on SLM1 to modulate the incident Gaussian beam from the collimator in experimental setup shown in Figure 8.
 |
Figure 8 Sketch of the experimental set-up for path-encoded matrix transformation. HWP: half wave plate, SLM: spatial light modulator, CCD: charge-coupled device camera. |
The experimental results are summarized in Figures 9A and 9B. The distributions of fidelity and success probability of implemented matrices are shown as solid bars, respectively. Here, the fidelity is evaluated by a charge coupled device (CCD) camera placed at the output port in the experimental setup shown in Figure 8. Since the target matrix  is unitary, the value of
is unitary, the value of  between
between  and implemented matrix
and implemented matrix  equals
equals  according to eq. (9).
according to eq. (9).
 (18)
(18)
 |
Figure 9 Experimental results of path-encoded matrix transformation. The distributions of (A) fidelity and (B) success probability for 80 different tests. The typical experimental results for (C) Hadamard matrix H3, (D) H2, and (E–H) some other unitary operators. For each group, there are the amplitude of target matrix U, the measured amplitude and the measured phase of implemented matrix V from left to the right. The color bar is also shown. |
The amplitude of  can be directly measured by the CCD camera. Actually, to measure
can be directly measured by the CCD camera. Actually, to measure  is a phase test. During the test, the input states of
is a phase test. During the test, the input states of  ,
,  and
and  are settled as the columns of target matrix
are settled as the columns of target matrix  . The results would also form an identical matrix if the implemented matrix
. The results would also form an identical matrix if the implemented matrix  is sufficiently accurate, as shown in Figures 9C–9H. The phase differences among diagonal elements of
is sufficiently accurate, as shown in Figures 9C–9H. The phase differences among diagonal elements of  are assumed to be zero during this estimation because subsequent phase shifters could be used for error correction [46]. Besides, according to eq. (2), the implementing errors of any diagonal matrix
are assumed to be zero during this estimation because subsequent phase shifters could be used for error correction [46]. Besides, according to eq. (2), the implementing errors of any diagonal matrix  would influence both relative phase within matrix rows and relative phase between matrix rows simultaneously. Thus, if the relative phase within matrix rows is accurate evidently, it is unlikely to remain a large relative phase between matrix rows.
would influence both relative phase within matrix rows and relative phase between matrix rows simultaneously. Thus, if the relative phase within matrix rows is accurate evidently, it is unlikely to remain a large relative phase between matrix rows.
The amplitude of  is scanned with input states
is scanned with input states  ,
,  and
and  , providing an intuitive vision of absolute value of matrix elements. The success probability is calculated by the output optical power from the three path-encoding channels normalized by the total output power received by the CCD camera.
, providing an intuitive vision of absolute value of matrix elements. The success probability is calculated by the output optical power from the three path-encoding channels normalized by the total output power received by the CCD camera.
The average value of fidelity is  among 80 different tests. The success probability is shown in Figure 9B with an average value of
among 80 different tests. The success probability is shown in Figure 9B with an average value of  . The main reason of deteriorated probability is that part of optical energy entered guard bands and failed to vanish through interference. The experimental results of
. The main reason of deteriorated probability is that part of optical energy entered guard bands and failed to vanish through interference. The experimental results of  gate and
gate and  gate (acting on the first and third channel) are shown in Figures 9C and 9D, respectively. The original data captured by CCD camera are also shown. As concrete examples, the data of another four typical unitary matrices are shown in Figures 9E–9H, while the fidelity value ranges from 0.96 to 0.99.
gate (acting on the first and third channel) are shown in Figures 9C and 9D, respectively. The original data captured by CCD camera are also shown. As concrete examples, the data of another four typical unitary matrices are shown in Figures 9E–9H, while the fidelity value ranges from 0.96 to 0.99.
A brief error analysis for experimental results is as follows. First, the conditioned maximum algorithm is utilized to determine the modulation functions of  ,
,  ,
,  . The fidelity values are conditioned by
. The fidelity values are conditioned by  . As a result, the average probability value tends to be lower than the average fidelity value. Second, a five-layer structure is sufficient for arbitrary
. As a result, the average probability value tends to be lower than the average fidelity value. Second, a five-layer structure is sufficient for arbitrary  matrices according to the decomposition theory [26]. Though the three-layer structure employed in this work is enough for most cases, the fidelity and probability could not both achieve 1 at the same time for some particular target matrices, hence there is a tradeoff. Third, experimental errors in terms of optical misalignment and nonlinear effects induced by CCD camera would also deteriorate both the fidelity and probability. The saturated effect of some CCD images will result in lower fidelity and efficiency estimation. The fidelity is calculated through phase test shown in Figures 9C and 9D. The saturated effect induces reduction of intensity of main lobs but has little influence on side lobs, thus lowers the weight of main lobs as well as the value of
matrices according to the decomposition theory [26]. Though the three-layer structure employed in this work is enough for most cases, the fidelity and probability could not both achieve 1 at the same time for some particular target matrices, hence there is a tradeoff. Third, experimental errors in terms of optical misalignment and nonlinear effects induced by CCD camera would also deteriorate both the fidelity and probability. The saturated effect of some CCD images will result in lower fidelity and efficiency estimation. The fidelity is calculated through phase test shown in Figures 9C and 9D. The saturated effect induces reduction of intensity of main lobs but has little influence on side lobs, thus lowers the weight of main lobs as well as the value of  . The detailed evaluation considering a
. The detailed evaluation considering a  case is below.
case is below.
After normalization, suppose that an averaged reduction of  is induced for all diagonal elements of
is induced for all diagonal elements of  due to saturation. At the same time, the difference among diagonal elements of
due to saturation. At the same time, the difference among diagonal elements of  would decrease by
would decrease by  . The
. The  value is comparable with
value is comparable with  value and we have
value and we have  if the derivative value of the saturation function is less than 1. According to the definition of fidelity in eq. (18), the numerator term of
if the derivative value of the saturation function is less than 1. According to the definition of fidelity in eq. (18), the numerator term of  would decrease by
would decrease by  , while the denominator term of
, while the denominator term of  would decrease from about
would decrease from about  to
to  , assuming that the values of diagonal elements of
, assuming that the values of diagonal elements of  are about 1. The denominator term would decrease by
are about 1. The denominator term would decrease by  , which is one order smaller than the reduction of numerator. The square root calculation in denominator further shrinks the reduction. Hence, the saturated effect will result in lower fidelity estimation.
, which is one order smaller than the reduction of numerator. The square root calculation in denominator further shrinks the reduction. Hence, the saturated effect will result in lower fidelity estimation.
The amplitude measurement shown in Figures 9C and 9D is used to evaluate transformation efficiency (success probability). The saturated effect lowers the measured optical power from the three path-encoding channels and decreases the efficiency value.
It could be concluded that the three-layer structure is valid to achieve both high fidelity and high success probability for most 3-dimensional unitary matrices. Thus, the experimental results of path-encoded unitary transformation are important evidence to prove the versatility of our OAM domain proposal.
DISCUSSION
First, the relations and differences between our work and the frequency-domain protocols are discussed. Our method shares the same basic mathematical theorem [25] of matrix decomposition with Lougovski’s work [27]. In their work, the frequency-time Fourier relation is employed. We notice that frequency encoding is different from other photonic encoding since energy conservation is not satisfied for unitary linear operations such as the Pauli  gate. Thus, it cannot be achieved by only passive setup. In this work, we focus on OAM and path domains employing the OAM-angle Fourier relation and the position-momentum Fourier relationship. Correspondingly, the unitary operations within both OAM and path domains could be implemented with passive optical elements.
gate. Thus, it cannot be achieved by only passive setup. In this work, we focus on OAM and path domains employing the OAM-angle Fourier relation and the position-momentum Fourier relationship. Correspondingly, the unitary operations within both OAM and path domains could be implemented with passive optical elements.
Next, a brief comparison between our proposal and previous approaches is made for both OAM-domain and path-domain. Different from other OAM-domain approaches, the cut-off effects from infinite OAM-encoding basis to finite subset are largely alleviated since ancillary guard bands are employed. During the unitary operation, part of the input energy would enter the guard bands, but such bands could be managed to vanish eventually through interference according to meticulous design. The number of required spectral shaper layers grows in O(N) scale according to dimensionality N of unitary operation. The reason is that each spectral shaper could provide O(N) modulation on all the channels in parallel, thus the whole setup can fulfill  independent real numbers required by a unitary operation. Compared with the MPLC approach [21,22,47], our design has similar system arrangement of O(N) layers as dimensionality
independent real numbers required by a unitary operation. Compared with the MPLC approach [21,22,47], our design has similar system arrangement of O(N) layers as dimensionality  grows. However, near-unity transformation efficiency and near-perfect fidelity can be achieved theoretically at the same time with our proposal according to the results of numerical simulations. Besides, our proposed scheme can perform parallel unitary operations on different OAM encoding channels simultaneously without increasing system arrangement. It should be mentioned that although our method is based on the mathematic decomposition of the Fourier/diagonal matrix, there is no DFT matrix required. Specifically, our proposed unitary operation scheme for OAM-domain is performed within OAM-domain and angle-domain alternately, while there is no actual DFT transformation between them. Actually, the OAM shaper is employed to perform the diagonal operation, while the DFT matrix is required for the MPLC method. However, since there is no requirement of DFT transformation, our scheme has to be performed within two optical DOF linked by Fourier transformation, e.g., the OAM-domain vs. angle-domain and path-domain vs. wavevector-domain.
grows. However, near-unity transformation efficiency and near-perfect fidelity can be achieved theoretically at the same time with our proposal according to the results of numerical simulations. Besides, our proposed scheme can perform parallel unitary operations on different OAM encoding channels simultaneously without increasing system arrangement. It should be mentioned that although our method is based on the mathematic decomposition of the Fourier/diagonal matrix, there is no DFT matrix required. Specifically, our proposed unitary operation scheme for OAM-domain is performed within OAM-domain and angle-domain alternately, while there is no actual DFT transformation between them. Actually, the OAM shaper is employed to perform the diagonal operation, while the DFT matrix is required for the MPLC method. However, since there is no requirement of DFT transformation, our scheme has to be performed within two optical DOF linked by Fourier transformation, e.g., the OAM-domain vs. angle-domain and path-domain vs. wavevector-domain.
For path-domain operation, both of our protocol and Reck’s scheme can be adopted and keep similar features of programmability, scalability, and near-unity success probability in theory, although they are based on different matrix decomposition. In this work, our experiment is based on three SLMs to perform the transformation. In our setup, the insertion loss of utilized three SLMs is about 11.9 dB. Thus, the scale of our experimental scheme would suffer from the insertion loss of the SLM since more SLMs are required for transformation with higher dimensionalities. It should be mentioned that our proposal is also manageable in both free space optics and integrated circuits. The SLMs could be replaced by three-dimensional set of metasurfaces [48] to achieve a compact and low-loss module for unitary operations. Due to the similar alignment of path channels in our proposal and Reck’s scheme, an on-chip version of our design could also be implemented. The key function of Fourier transform could be achieved by the structures of Rowland circle according to the recently reported work [49]. Note that in this design no MMI couplers [29] nor fully connective  blocks [30] are needed. Our proposal would provide an alternative choice in addition to the reported integrated architectures [29,30].
blocks [30] are needed. Our proposal would provide an alternative choice in addition to the reported integrated architectures [29,30].
In conclusion, we have proposed and demonstrated a scheme for unitary operation in OAM and optical path domains. A three-layer setup is implemented to evaluate the performance. Field simulation of OAM-domain Hadamard matrices and experimental implementation of randomly generated path-domain unitary matrices have been carried out. For path domain, the fidelity value of  and transformation efficiency of
and transformation efficiency of  are experimentally evaluated simultaneously.
are experimentally evaluated simultaneously.
Acknowledgments
The authors would like to thank Dr. Peng Zhao in Appotronics Corporation Ltd. for valuable discussions and helpful comments.
Funding
This work was supported by the National Key Research and Development Program of China (Grant Nos. 2018YFB2200402 and 2017YFA0303700), the National Natural Science Foundation of China (Grant No. 61875101), the Beijing Academy of Quantum Information Science, the Beijing National Research Center for Information Science and Technology (BNRist), the Beijing Innovation Center for Future Chip, and the Tsinghua University Initiative Scientific Research Program.
Conflict of interest
The authors declare that they have no conflict of interest.
References
- Bogaerts W, Pérez D, Capmany J, et al. Programmable photonic circuits. Nature 2020; 586: 207-216. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Carolan J, Harrold C, Sparrow C, et al. Universal linear optics. Science 2015; 349: 711-716. [Article] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Wang J, Paesani S, Ding Y, et al. Multidimensional quantum entanglement with large-scale integrated optics. Science 2018; 360: 285-291. [Article] [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Li S, Zhang S, Feng X, et al. Programmable coherent linear quantum operations with high-dimensional optical spatial modes. Phys Rev Appl 2020; 14: 024027. [Article] [CrossRef] [Google Scholar]
- Allen L, Beijersbergen MW, Spreeuw RJC, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A 1992; 45: 8185-8189. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kulkarni G, Sahu R, Magaña-Loaiza OS, et al. Single-shot measurement of the orbital-angular-momentum spectrum of light. Nat Commun 2017; 8: 1054. [Article] [CrossRef] [PubMed] [Google Scholar]
- Mair A, Vaziri A, Weihs G, et al. Entanglement of the orbital angular momentum states of photons. Nature 2001; 412: 313-316. [Article] [CrossRef] [PubMed] [Google Scholar]
- Malik M, Erhard M, Huber M, et al. Multi-photon entanglement in high dimensions. Nat Photon 2016; 10: 248-252. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Uribe-Patarroyo N, Fraine A, Simon DS, et al. Object identification using correlated orbital angular momentum states. Phys Rev Lett 2013; 110: 043601. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fickler R, Lapkiewicz R, Plick WN, et al. Quantum entanglement of high angular momenta. Science 2012; 338: 640-643. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Reck M, Zeilinger A, Bernstein HJ, et al. Experimental realization of any discrete unitary operator. Phys Rev Lett 1994; 73: 58-61. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Yu J, Zhou C, Jia W, et al. Three-dimensional Dammann vortex array with tunable topological charge. Appl Opt 2012; 51: 2485. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Deng D, Li Y, Han Y, et al. Perfect vortex in three-dimensional multifocal array. Opt Express 2016; 24: 28270. [Article] [CrossRef] [PubMed] [Google Scholar]
- Mehmood MQ, Mei S, Hussain S, et al. Visible-frequency metasurface for structuring and spatially multiplexing optical vortices. Adv Mater 2016; 28: 2533-2539. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jin Z, Janoschka D, Deng J, et al. Phyllotaxis-inspired nanosieves with multiplexed orbital angular momentum. eLight 2021; 1: 5. [Article] [CrossRef] [Google Scholar]
- Ni J, Huang C, Zhou LM, et al. Multidimensional phase singularities in nanophotonics. Science 2021; 374: eabj0039. [Article] [CrossRef] [PubMed] [Google Scholar]
- Babazadeh A, Erhard M, Wang F, et al. High-dimensional single-photon quantum gates: Concepts and experiments. Phys Rev Lett 2017; 119: 180510. [Article] [CrossRef] [PubMed] [Google Scholar]
- Gao X, Krenn M, Kysela J, et al. Arbitrary d-dimensional Pauli X gates of a flying qudit. Phys Rev A 2019; 99: 023825. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine NK, Ryf R, Chen H, et al. Laguerre-Gaussian mode sorter. Nat Commun 2019; 10: 1865. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schlederer F, Krenn M, Fickler R, et al. Cyclic transformation of orbital angular momentum modes. New J Phys 2016; 18: 043019. [Article] [CrossRef] [Google Scholar]
- Brandt F, Hiekkamäki M, Bouchard F, et al. High-dimensional quantum gates using full-field spatial modes of photons. Optica 2020; 7: 98. [Article] [CrossRef] [Google Scholar]
- Labroille G, Denolle B, Jian P, et al. Efficient and mode selective spatial mode multiplexer based on multi-plane light conversion. Opt Express 2014; 22: 15599. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Slussarenko S, Karimi E, Piccirillo B, et al. Universal unitary gate for single-photon spin-orbit four-dimensional states. Phys Rev A 2009; 80: 022326. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Li S, Zhao P, Feng X, et al. Measuring the orbital angular momentum spectrum with a single point detector. Opt Lett 2018; 43: 4607. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schmid M, Steinwandt R, Müller-Quade J, et al. Decomposing a matrix into circulant and diagonal factors. Linear Algebra its Appl 2000; 306: 131-143. [Article] [CrossRef] [MathSciNet] [Google Scholar]
- Huhtanen M, Perämäki A. Factoring matrices into the product of circulant and diagonal matrices. J Fourier Anal Appl 2015; 21: 1018-1033. [Article] [CrossRef] [MathSciNet] [Google Scholar]
- Lukens JM, Lougovski P. Frequency-encoded photonic qubits for scalable quantum information processing. Optica 2017; 4: 8. [Article] [CrossRef] [Google Scholar]
- Lu HH, Lukens JM, Peters NA, et al. Electro-optic frequency beam splitters and tritters for high-fidelity photonic quantum information processing. Phys Rev Lett 2018; 120: 030502. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tang R, Tanemura T, Nakano Y. Integrated reconfigurable unitary optical mode converter using MMI couplers. IEEE Photon Technol Lett 2017; 29: 971-974. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Saygin MY, Kondratyev IV, Dyakonov IV, et al. Robust architecture for programmable universal unitaries. Phys Rev Lett 2020; 124: 010501. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Yao E, Franke-Arnold S, Courtial J, et al. Fourier relationship between angular position and optical orbital angular momentum. Opt Express 2006; 14: 9071-9076. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Forbes A, Dudley A, McLaren M. Creation and detection of optical modes with spatial light modulators. Adv Opt Photon 2016; 8: 200. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Staude I, Schilling J. Metamaterial-inspired silicon nanophotonics. Nat Photon 2017; 11: 274-284. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Pinnell J, Rodríguez-Fajardo V, Forbes A. Single-step shaping of the orbital angular momentum spectrum of light. Opt Express 2019; 27: 28009. [Article] [CrossRef] [PubMed] [Google Scholar]
- Berkhout GCG, Lavery MPJ, Courtial J, et al. Efficient sorting of orbital angular momentum states of light. Phys Rev Lett 2010; 105: 153601. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lavery MPJ, Robertson DJ, Berkhout GCG, et al. Refractive elements for the measurement of the orbital angular momentum of a single photon. Opt Express 2012; 20: 2110. [Article] [CrossRef] [PubMed] [Google Scholar]
- Potoček V, Miatto FM, Mirhosseini M, et al. Quantum Hilbert hotel. Phys Rev Lett 2015; 115: 160505. [Article] [CrossRef] [PubMed] [Google Scholar]
- Mirhosseini M, Malik M, Shi Z, et al. Efficient separation of the orbital angular momentum eigenstates of light. Nat Commun 2013; 4: 2781. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Leach J, Padgett MJ, Barnett SM, et al. Measuring the orbital angular momentum of a single photon. Phys Rev Lett 2002; 88: 257901. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zhao P, Li S, Feng X, et al. Measuring the complex orbital angular momentum spectrum of light with a mode-matching method. Opt Lett 2017; 42: 1080. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Clements WR, Humphreys PC, Metcalf BJ, et al. Optimal design for universal multiport interferometers. Optica 2016; 3: 1460. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- D′Ambrosio V, Carvacho G, Agresti I, et al. Tunable two-photon quantum interference of structured light. Phys Rev Lett 2019; 122: 013601. [Article] [CrossRef] [PubMed] [Google Scholar]
- Wang XY, Zhao SH, Dong C, et al. Orbital angular momentum-encoded measurement device independent quantum key distribution under atmospheric turbulence. Quantum Inf Process 2019; 18: 304. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Wen Y, Chremmos I, Chen Y, et al. Spiral transformation for high-resolution and efficient sorting of optical vortex modes. Phys Rev Lett 2018; 120: 193904. [Article] [CrossRef] [PubMed] [Google Scholar]
- Yang Y, Zhao Q, Liu L, et al. Manipulation of orbital-angular-momentum spectrum using pinhole plates. Phys Rev Appl 2019; 12: 064007. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Rahimi-Keshari S, Broome MA, Fickler R, et al. Direct characterization of linear-optical networks. Opt Express 2013; 21: 13450. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Morizur JF, Nicholls L, Jian P, et al. Programmable unitary spatial mode manipulation. J Opt Soc Am A 2010; 27: 2524. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Faraji-Dana MS, Arbabi E, Arbabi A, et al. Compact folded metasurface spectrometer. Nat Commun 2018; 9: 4196. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cheng R, Zou CL, Guo X, et al. Broadband on-chip single-photon spectrometer. Nat Commun 2019; 10: 4104. [Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Figures
 |
Figure 1 The scheme of OAM-domain unitary operation with three-layer. |
| In the text | |
 |
Figure 2 Simulations of OAM spectral shaper with Huygens-Fresnel principle. (A) The scheme of OAM spectral shaper. (B) Step-by-step field evolution of an initial superposed OAM state passing through the spectral shaper. (C) Initial OAM spectrum. (D) Output OAM spectrum. The brightness and color indicate the amplitude and phase distributions, respectively. |
| In the text | |
 |
Figure 3 Optimized approach for OAM-domain Hadamard matrices with dimensionality of |
| In the text | |
 |
Figure 4 Fidelity and probability of unitary transformation as functions of numbers of guard bands. The target matrices are chosen as |
| In the text | |
 |
Figure 5 Step-by-step field evolution of OAM-domain Hadamard matrix. |
| In the text | |
 |
Figure 6 The OAM-domain parallel |
| In the text | |
 |
Figure 7 (A) Conceptual set-up of path-encoded matrix transformation, and the modulation functions settled on SLMs. (B) Optimized phase modulation function settled on SLM2 for implementing |
| In the text | |
 |
Figure 8 Sketch of the experimental set-up for path-encoded matrix transformation. HWP: half wave plate, SLM: spatial light modulator, CCD: charge-coupled device camera. |
| In the text | |
 |
Figure 9 Experimental results of path-encoded matrix transformation. The distributions of (A) fidelity and (B) success probability for 80 different tests. The typical experimental results for (C) Hadamard matrix H3, (D) H2, and (E–H) some other unitary operators. For each group, there are the amplitude of target matrix U, the measured amplitude and the measured phase of implemented matrix V from left to the right. The color bar is also shown. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.





































