| Issue |
Natl Sci Open
Volume 2, Number 6, 2023
|
|
|---|---|---|
| Article Number | 20220051 | |
| Number of page(s) | 13 | |
| Section | Information Sciences | |
| DOI | https://doi.org/10.1360/nso/20220051 | |
| Published online | 31 March 2023 | |
RESEARCH ARTICLE
Information overload: How hot topics distract from news—COVID-19 spread in the US
1 Computational Communication Collaboratory, Nanjing University, Nanjing 210093, China
2 Complex Systems Group, Department of Mathematics and Statistics, The University of Western Australia, Perth 6009, Australia
3 School of Media and Communication, Shenzhen University, Shenzhen 518060, China
* Corresponding authors (emails: binyang.nju@hotmail.com (Bin Yang); kekeshang@nju.edu.cn (Ke-ke Shang); michael.small@uwa.edu.au (Michael Small); npchao@szu.edu.cn (Naipeng Chao))
Received:
28
September
2022
Revised:
29
November
2022
Accepted:
5
December
2022
Information dissemination and the associated change of individual behavior can significantly slow the spread of an epidemic. However, major social events which attract public attention will disturb information spread and affect epidemic transmission in ways that have not been readily quantified. We investigate the interplay between disease spreading and disease-related information dissemination in a two-layer network. We employ the SIR-UAU model with a time dependent coefficient to denote information dissemination. We found that major social events are equivalent to perturbations of information dissemination in certain time intervals and will consequently weaken the effect of information dissemination, and increase prevalence of infection. Our simulation results agree well with the trends observed from real-world data sets. We found that two specific major events explain the trend of the coronavirus epidemic in the US: the online propaganda and international agenda setting of Donald Trump early in 2020 and the 2020 US Presidential Election.
Key words: information spreading / COVID-19 / SIR model / 2020 US Presidential Election / Altmetric / network propagation
© The Author(s) 2023. Published by Science Press and EDP Sciences
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
INTRODUCTION
Disease-related information will spread rapidly when an infectious disease breaks out. Those individuals who receive more information will become more aware of the disease and may consequently change their behavior[1]—such as being more willing to wear masks, to maintain physical distance and so on. In turn, those measures can slow the epidemic spreading process[2-6]. From the perspective of network structure, the topology of information dissemination and epidemic spreading are often different as individual awareness may be affected more by online social networks, such as Twitter and Facebook, and mass media rather than word of mouth [7, 8]. Correspondingly, the two-layer network provides a natural way to describe human interactions that occur in various scenarios, and can further accurately analyze the interaction between information dissemination of a certain epidemic awareness, and the epidemic spreading itself [7-15]. Thus, we adopt the two-layer network—one for information dissemination and the other for epidemic spreading—as our approach to explore that phenomenon.
Previous work has investigated the dynamics of the dissemination of disease-related information and disease spreading on two-layer networks: one for the network of physical contacts, the other for virtual communication. There is a one-to-one mapping between nodes in these two layers, to represent the same individual in each layer. The edges in the two layers represent different connectivity. Well-known models such as the Susceptible-Infected-Susceptible (SIS) model[16] and the Susceptible-Infected-Recovered (SIR) model[17] have been used to analyse epidemic spreading processes in the physical contact layer. Processes such as Unaware-Aware-Unaware (UAU) and Unaware-Aware (UA) have been introduced to investigate the information dissemination process that will generate new aware individual [7, 18]. Some of these studies have extended the model and discussed the factors that influence the mitigation effect of information dissemination such as behavior changing after receiving the information of infected individuals [19], individual heterogeneity[14], and self-initiated awareness mechanism[13].
The information dissemination rate is usually constant[7, 15]. However, these studies do not consider the complex and competitive media environment, and accompanying problem such as fake news[20-22] and attention distraction[23]. Modelling and estimating of events disruptive to scientific information dissemination under a pandemic is critical to our understanding of these issues, as well as for potential applications in future scenarios, such as providing reference for adjusting the setting of scientific information dissemination agenda under a pandemic [24, 25].
Specifically, as depicted in Figure 1, when some big events occur during a pandemic—for example, the 2020 US Presidential Election during the COVID-19 pandemic—individual focus may be shifted to those big events, and information about diseases would also be diverted due to agenda setting and preferential transmission within online social networks. In effect, the capacity for individuals to take in new information is bounded, and non-pandemic related news distracts from the capacity for protective behavior-altering information related to the pandemic. This may result in a significant drop in the probability of information dissemination for all individuals in some time intervals. Based on this assumption, we combined the SIR-UAU model with a time dependent coefficient to denote the information dissemination, and a drop in the information dissemination rate would be assigned to time intervals with big events to model the associated change of individual behavior on information spreading.
 |
Figure 1 A sketch to demonstrate our model. First, scientific information related to the disease spreads with a higher probability during an epidemic, and people who receive it will be more aware of the disease, becoming less susceptible to infection. However, while a major social event occurs during the epidemic, people’s attention will be diverted from scientific information to the social event, with lower probability for the scientific information spreading. People are therefore less likely to become aware, making them more susceptible to infection. |
For reasonable inference [26-28], it is important to compare the model to the real-world setting. However, it is challenging because there are several sources of uncertainty. Fortunately, consistency between real-world data and model inferences across multiple data sets could be a strong indicator of model interpretation validity. In this report, we used three real-world data sets: (1) cumulative confirmed diagnoses data in the US as the disease spread layer, (2) retweets of COVID-19-related articles on Twitter are considered as the information transmission layer, and (3) hashtags data on Twitter to examine the consistency of events inferred by the model.
We find that the two-layer network constructed from our model with two postulated events agrees well with the evolution of cumulative confirmed diagnoses data in the US (compared with disease spread layer) and retweets data of COVID-19-related articles on Twitter (compared with information transmission layer). In addition, the competition effect of the two events generated by the data of popularity of hashtags on Twitter also yields consistent results. In particular, simulation results indicate that the first big event occurred between March 2020 and June 2020—possibly triggered by the domestic political agitation of Donald Trump on Twitter (aimed primarily at blaming the coronavirus transmission on various groups external to the US, and at political opponents domestically). Here, the agenda setting in online social networks means that the most followed users on Twitter deliver speeches, and that a high volume of Twitter activity is focused on these small number of users. At the beginning of COVID-19 outbreak in the US, Donald Trump strove to guide the public opinion to the debate over epidemic source, severity and response—instead of providing scientific information useful for the rational appraisal of an emerging epidemic.
The second of these big events coincided with the lead up to the 2020 US Presidential Election—matching a significant drop in the number of retweets of COVID-19 related articles on Twitter. In addition, the initiation and the end of the election event, representing the decline and rebound of the information dissemination rate, correspond to two substantial perturbations in the total confirmed cases of the United States.
MODEL FOR AWARENESS-EPIDEMIC WITH BIG EVENTS
We use a two-layer network to describe the two spreading processes: The epidemic SIR model is used to model the dynamics of spreading in the contact layer while the process UAU models the information spreading process. As shown in Figure 2A, the nodes in the upper (information) layer may have two states (i.e., aware or unaware), and the lower (epidemics) layer may have three states (i.e., susceptible, infected, recovered). At the same time, we assume that when individuals are infected, they will directly enter the aware (A) state. Therefore, in this SIR-UAU model, an individual can be in four states as the following: unaware susceptible (SU), aware susceptible (SA), aware infected (IA) and aware recovered (RA). Figure 2B presents the possible transitions among the four states. We note, somewhat unapologetically that these models are nothing more than a caricature of the underlying disease transmission process. Our aim here is to propose a simple model with few parameters that, nonetheless, captures the interplay between information and infection.
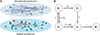 |
Figure 2 The sketch of the two-layer network used in our SIR-UAU model and the schematic illustration of the SIR-UAU dynamics in that two-layer network. (A) The upper layer represents the information dissemination, where each node has two possible states: aware (A, blue nodes) or unaware (U, gray nodes). The lower layer represents the physical contact network, in which nodes have three possible states: susceptible (S, green nodes), infected (I, red nodes) or recovered (R, pink nodes). There is a one-to-one mapping between nodes in two layers, to represent the same individual in each layer. (B) The upper row presents the unaware SIR and the lower row corresponds to the aware SIR. |
In the epidemic spreading process, at each time step Δt=1, the unaware susceptible individuals may be infected when they encounter infected individuals in the contact layer with disease spreading rate β. Susceptible individuals in the aware state will reduce their risk of being infected, and as a result, the probability of being infected will be reduced to (1-η) β, where η (with 0<η≤1) represents the infection reduction rate of aware individuals. All infected individuals will recover with a recovery rate γ.
Meanwhile, at each time step, the transition for an individual from unaware state to aware state occurs in the following two situations. First, infected persons will immediately enter the aware state. Second, the person who connects to aware individuals in the information dissemination layer, would enter the aware state at information spreading rate κ. All aware susceptible individuals will turn back to unaware state with an information decaying rate κ’. We assume that the susceptible individual is most aware when he/she just becomes aware, and as such awareness may decrease over time, and may eventually return to the unaware states.
However, this is the case under the normal situation without the distraction of “off-topic” big events. When big events occur, the flow of disease-related information may decrease, or individuals may shift focus. Hence, we assume that the probability of receiving useful (and potentially protective) disease-related information will reduce to (1-I)κ, where I (with 0<I≤1) represents the competition effect (or intensity) of the event. After the event, the information spreading rate returns to κ.
SIMULATION
We considered a multiplex network composed by two-layer scale-free networks with N=5000 nodes each. Due to the high density of the real online social network (our model is based on a study of Twitter), we assume that the information dissemination network is constructed as a network with more links than the contact network. Two networks are generated independently, taking average degree (average number of contacts under scrutiny) 〈k〉=6 for the epidemic spreading network, which is close to the value that [29] assumed in their analysis, and taking average degree (such as the average number of followers) 〈k〉=14 for the information dissemination network, which is close to the value in ref. [30]. Figure 2A presents the sketch of these two networks. At the initial state of each realization, 0.2% of the nodes are randomly chosen to assign with the state of IA (infected-aware), and other nodes are set to the SU state (susceptible-unaware).
To illustrate the possible impact of the emergence of big events, we perform a parameter sensitivity analysis. We first consider a simple case with only one big event starting at time t=15 with I=0.9 and duration of 8 time steps. Comparing the blue line and the orange line in Figure 3A, it is clear that information dissemination has a significant mitigating effect on disease transmission, and the occurrence of big event will weaken this mitigating effect of information dissemination. Obviously, the event will immediately lead to the rise of infected cases, as depicted by the green line in Figure 3A. The overall infection rate increased by 22.1% at t=30, and as the big event also brought the turning point earlier, the overall infection rate increased by 11.9% in the end of the epidemic.
 |
Figure 3 Simulated comparison of (A) the number of new infected and (B) the number of new aware as a function of time step t for disease spreading under three cases: without information dissemination (blue dashed line); disease spreading with information dissemination at rate κ=0.15 (orange solid line), and disease spreading with information dissemination at rate κ=0.15 and with one event starting at time t=15 with competition effect I=0.9 and duration of 8 time steps (green dotted line). In three cases we always set the information decaying rate κ’=0.2, the infection reduction rate η=0.85, the disease spreading rate β=0.15 and the recovering rate γ=0.1. Colored bands show the 1σ confidence interval of our prediction. |
To study the disturbance from big event, we set κ and β to different values and analyze the final infection rate for two cases, SIR-UAU without event and SIR-UAU with one event. As shown in Figure 4A and 4B, for the small information dissemination rate κ, the infected rate would raise rapidly with the increase of disease spreading rate β. But while increasing the information dissemination rate κ, the impact of the disease transmission rate β on overall infected rate would become less significant. In Figure 4C, the net effect of the event on the total infected rate is shown. And the effect of big event is more significant when the information dissemination rate κ and the disease spreading rate β are small.
 |
Figure 4 The effect of the disease spreading rate β, the information dissemination rate κ and one event on the total infected rate. (A) two-layer network of disease spreading and information dissemination without event. (B) two-layer network of disease spreading and information dissemination with one event, starting at time t=0 with competition effect I=0.9 and duration of 8. In two cases we always set the information decaying rate κ’=0.2, the infection reduction rate η=0.85 and the recovering rate γ=0.1. (C) The net effect of one event on the total infected rate, which shows the effect of the event is more significant when the information dissemination rate κ and the disease spreading rate β are both small. For the image processing, the Gaussian smoothing algorithm with σ=1.5 was used. |
Furthermore, to investigate the degeneracy among these parameters, we explore four sets of the disease spreading rate β, the recovering rate γ and event duration Δt, and vary the competition effect I (I∈[0,1]) and different start time t (t∈[0,50]) of the event. Figure 5 depicts the net effect of the event on the total infected rate. In all cases considered, the competition effect and the start time of the big event could significantly affect the total infected rate. In general, when the competition effect I of the event is lower than 0.4, the impact of the event on the total infections will not be obvious. And we also found that the factor of different start times of the event may be affected by the speed of the spread of disease and information. The event that occurs at the beginning of disease transmission (t~[0, 3]) would have the greatest effect, and at that time, information spreads most rapidly. As shown in Figure 3B, the dissemination of information will decline rapidly afterwards, and then remain at a relatively low level. For the event that occurred around t~[4, 9], as shown in Figure 3, the speed of information dissemination and disease spreading was both relatively low at that time, and the impact of the event was much weaker. As the disease spread accelerates, the impact of the event will rise again. See SIR-UAU line (orange solid line) in Figure 3A and Figure 6B, the turning point of disease transmission corresponds to the second peak of the impact of the event at t ~ 22. Finally, as the slowing down of disease transmission, the impact of the event will gradually weaken.
 |
Figure 5 Under four sets of parameters, the effect of event start time t (t∈[0,100]) and event competition effect I (I∈[0,1]) on net effect on the total infected rate of the event. In all cases we always set the information dissemination rate κ=0.15, the information decaying rate κ’=0.2 and the infection reduction rate η=0.85. For the image processing, the Gaussian smoothing algorithm with σ=1.5 was used. |
 |
Figure 6 SIR-UAU two-layer network with two events to simulate from empirical data. Using data of (A) cumulative confirmed cases of United States; (B) the retweets of the COVID-19 related research papers on Twitter, depicts by the blue diamond points. The green line and the orange line correspond to the simulation results with and without the two big media events, respectively. The simulation results of the information dissemination layer are based on the hypothesis that the amount an individual will output information when entering the aware state is p=n-0.3, where n is the number of times that individual turning to aware state. Two big events are added to the two-layer network model, one is starting in the beginning, with competition effect I=0.45 and duration Δt=8, another is starting at time t=17, with I=0.87 and duration Δt=8. In the two-layer network, the disease spreading rate β=0.07, the information dissemination rate κ=0.15, the recovering rate γ=0.11, the information decaying rate κ’=0.2 and the infection reduction rate η=0.85. Color band shows the 1σ confidence interval of our prediction. |
COVID-19 SPREADING IN THE US
We investigated the model based on the COVID-19 spread and virus-related information dissemination trends in the United States, to demonstrate the possible effect of the big event during the epidemic, and to explore the potential applicability of our framework in other scenarios.
We used the cumulative confirmed cases of US reported by Johns Hopkins University in the disease spreading layer. In the information dissemination layer, we employ the data of retweets of the academic papers which mention COVID-19 on Twitter (searching key word is COVID-19, from March 2020 to March 2021, source from Altmetrics.com). We treat COVID-19 related scientific literature as a proxy for all COVID-19 relevant information. Naturally, since users that have tweeted journal articles included both academic users and non-academic users, it is difficult to exclude the influence of academic users. In order to compare our simulation results with information spreading of general users, as an approximation, we assume that the number of tweets from academic users is more consistent than that of non-academic users, and we scale the simulation results to the data that have been subtracting 3.4×105 tweets per month, which represents a stable output from academic users.
As shown in Figure 6, we can observe two breaks in the cumulative coronavirus diagnosis numbers of the US and a drop in the retweet data, both happened around the end of 2020. This is exactly what we would expect from the anticipation effect of a big event as discussed before. Therefore, we tune parameters of our two-layer network with the big events, and investigate if our model could consistently explain features observed in the real-world network. As shown in Figure 6, the simulation results of the two-layer model combined with two big events match the evolution trend of the real-world data (The value of the coefficient of determination R2 1 for the model fit to the confirmed cases data is 0.98), especially the two breaks in confirmed cases in November 2020 and January 2021. The first event, which occurs between t=0 (March 2020) and t=8 (June 2020) with lower competition effect I=0.45, may represent the mass media or information in social networks focusing on other parts of the world while the epidemic breaks out, and the most significant event is Donald Trump’s Twitter agenda setting around that time—his attempts to simultaneously both externalise and diminish the effect of coronavirus, largely via Twitter. For the second event, which occurs between t=17 (October 2020) and t=25 (January 2021) with very high competition effect I=0.87, we link this to the 2020 US Presidential Election at the end of 2020.
When comparing the simulation of information dissemination layer with the retweets of COVID-19 related articles, we found that the first event (0<t<8) catches the decline of the retweet data of COVID-19 literature around June 2020 and a rebounding component followed closely thereafter. The second big event (17<t<25), due to its strong competition effect, leads to a very slow information dissemination, which corresponds to a significant drop of retweet data from October 2020 to January 2021.
In order to examine the consistency of the two possible events, we further explored the evolution of related hashtags on Twitter (Figure 7). Here we use the hashtag #COVID-19 to represent disease-related information dissemination, hashtags #Chinesevirus and #Chinavirus to represent the confusion caused by Donald Trump in the initial stage of the epidemic, and hashtag #Election2020, the most used hashtag under the event, to represent the US Presidential Election. Figure 7A depicts the trend of the hashtags of related events on Twitter2, which is consistent with the inference of our model (gray area).
 |
Figure 7 (A) Evolution of the popularity of hashtags corresponding to two possible events and COVID-19-related information on Twitter. (B) Competition effect I calculated by popularity of the hashtags of #COVID, #Election2020, #Chinesevirus and #Chinavirus. We assume I equals to the popularity of the hashtags of the two events divided by the sum of the popularity of the hashtags of two events and the popularity of hashtag #COVID-19. (C), (D) SIR-UAU two-layer network simulated from empirical data, where the information dissemination rate is completely obtained from the hashtags of the possible two events. The diamond points depict the data of (A) cumulative confirmed cases of US; (B) the retweets of the COVID-19 related research papers on Twitter. And the green line and the orange line correspond to the simulation results with and without the two big media events, respectively. In the two-layer network, the parameters we set are consistent with the previous method, in which disease spreading rate β=0.07, information dissemination rate κ=0.15, recovering rate γ=0.11, information decaying rate κ’=0.2 and infection reduction rate η=0.85. Color band shows the 1σ confidence interval of our prediction. |
We assume that when an event grabs the attention from COVID-19-related information, its competition effect I approximately equals the popularity of the event divided by the sum of the popularity of the event and the popularity of the disease-related information. We analyze the popularity of hashtags from 9 March 2020 to 31 May 2020 (the first event) and that of 5 October 2020 to 3 January 2021 (the second event), then estimate the competitive effects of the two events. The calculated competition parameter of the first event is 0.438, and the calculated competition parameter of the second model event is 0.861. The result is consistent with the model inference, 0.45 and 0.87, respectively.
In addition, if the information dissemination rate is always dominated by the competition effect brought by these two events, as shown in Figure 7B. The fitting of the two-layer network based on this information dissemination rate with the real-world two-layer network is consistent with the previous method (The value of the coefficient of determination R2 for the model fit to the confirmed cases data is 0.92). Note that there is a deviation around July in the information dissemination (as shown in Figure 7C). However, since the statistics from May to September are quite small, as shown in Figure 7A, this deviation could be caused by statistical errors.
CONCLUSION AND DISCUSSION
In this report, we present a novel awareness-epidemic model to explore the interplay between transmission of information that may inform protective practise, and irrelevant “hot topics" which act as noise and dilute the available bandwidth for helpful signal. We have shown that the model matches both qualitatively and quantitatively the events surrounding the 2020 COVID-19 outbreak in the US and the concurrent political environment. Our model provides a plausible explanation—consistent with data—for the timing and relative severity of the 2020 COVID-19 waves in the US. The practical consequences of this are two-fold. First, in a general sense our work provides a cautionary lesson around the effect of distracting from important public health messages. Second, it provides a more concrete way to understand the link between the timing of protective information dissemination and infection. Lessons from this modelling have been used by at least one of our governments to better manage the control of COVID-19 in their own jurisdiction [32].
Specifically, the addition of big (distracting) events in the epidemic-awareness network will divert individual attention and weaken the mitigation effect on disease spreading. The higher competition effect of the big event, the mitigation effect would be weaker. And we find that the effect of the big event was more prominent in the following time period. One is at the early stage of the epidemic, when most people had not yet entered aware state, and the information spread very fast at that time, therefore the impact during this period is most prominent. The other would occur at time after the spread of information slowing down. During that time, the impact of the event will rise again due to the acceleration of the spread of the disease, and the impact will reach its peak again at the turning point of the epidemic. This suggests that reducing the intensity of the broadcast of big events can be helpful to lower the interference of big events on the dissemination of information, especially for big events occurred in the early-stage and around the turning point of the epidemic. That is, diversity of news subjects will better allow for clear communication of virus-related information.
More importantly, using the example of COVID-19 outbreak in the US, we compare our inference based on two events with real-world data. We found that the simulation results could capture the trajectory of cumulative confirmed diagnoses data in the US (compared with disease spread layer) and retweets data of COVID-19-related articles on Twitter (compared with information transmission layer). Due to coincidence of time, we speculate one of the big events may be linked to the 2020 US Presidential Election.
Clearly the dissemination of COVID-19 related articles on Twitter provides an important reference for the starting time, duration, and competition effect of the big events. However, the competition effect of the first event is relatively low (I=0.45), therefore it is more difficult to accurately estimate its starting time and duration. Hence, we had tried to include another big event — the “Black Lives Matter” protests and social unrest, which happened around June 2020, to represent the first event. Since these events happened later than Donald Trump’s Twitter agenda setting in early stage of 2020, we could catch the trend of retweet data only when the probability of information dissemination κ is relatively low (<0.1). While in this way, it will be difficult to catch the two breaks in the cumulative diagnosis of US on the disease transmission layer.
We also tried to use three big events in our framework, that is, adding the “Black Lives Matter” protest to the two prior events to simulate the two-layer network. Figure 8B and 8C show simulations based on the three events. We assumed that the rate of information dissemination is always dominated by the competition effects brought by these three events, and here we use the hashtag #blm to represent “Black Lives Matter" protest. Obviously, the simulation results deviate significantly from the real-word two-layer data compared with the simulation results of the two events. In addition, in terms of trends, as shown in Figure 8A, the popularity of #blm was very high in June. However, at the same time, the trend of the real-world information dissemination was on the rise, which is contrary to the possible competition effects of “Black Lives Matter" protest. Hence the “Black Lives Matter" would not have a significant competition effect on the spread of virus-related information.
 |
Figure 8 (A) Evolution of the popularity of hashtags #blm on Twitter. (B), (C) SIR-UAU two-layer network simulated from empirical data, where the information dissemination rate is completely obtained from the hashtags of the possible three events. The diamond points depict the data of (A) cumulative confirmed cases of US; (B) the retweets of the COVID-19 related research papers on Twitter. And the green line and the orange line correspond to the simulation results with and without the two big media events, respectively. In the two-layer network, the parameters we set are consistent with the previous method, in which disease spreading rate β=0.07, information dissemination rate κ=0.15, recovering rate γ=0.11, information decaying rate κ’=0.2 and infection reduction rate η=0.85. Color band shows the 1σ confidence interval of our prediction. |
We caution that our interpretation ignores the time dependence of other mitigation strategies such as public intervention, and is only based on simulation with two events. As always, correlation is not causation, and our work is not intended as a direct attempt to implicate Mr. Trump or infer culpability based on his actions. However, public intervention, which escalates with the evolution of the epidemic, is difficult to interpret as a mechanism for increase in relative diagnosis numbers, while our framework with two big events provides a simpler explanation. There are other possible reasons for an acceleration in the cumulative diagnosis, such as the emergence of super spreaders, which however cannot explain the decline in information dissemination we have observed simultaneously. Furthermore, super-spreaders tend to be geographically localised and homogeneously distributed in time (while we could focus on isolated well-documented super-spreader events, plausible super-spreader events have been occurring relatively frequently, especially in the US. Hence, it is more natural that occurrence of big events will lead to an acceleration in disease spreading, as our framework suggests. First, the interplay between spreading of disease-related information and epidemic spreading is observed empirically. Second, it also indicates the important role that spreading of disease-related information plays in mitigation of an epidemic. The impact of big events on the epidemic should not be ignored. As indicated in Figure 6, for the case of absence of big event, depicted by orange dashed line, the disease prevalence is much lower than the case with two events. Considering scarce medical resources, the occurrence of big events also increases the risk of medical system breakdown.
R2 is the most widely used metric for regression problem in the study of human behaviour [31].
Data availability
Data on COVID-19 cases are publicly available through Johns Hopkins University (https://coronavirus.jhu.edu/us-map). Data on popularity of hashtags of Twitter are publicly available through trendsmap (https://www.trendsmap.com/). The above data can also be obtained from the corresponding author upon request. Data on retweets of COVID-19-related articles on Twitter was acquired through Altmetric (https://www.altmetric.com/), and is not publicly available.
Acknowledgments
We thank Altmetric.com for providing the altmetric data of scientific publications and B.Y. would like to thank Xiaoyuan Huang, Yijun Ran, Yunsong Chen, Junhan Yang and Cheng-jun Wang for helpful discussions and comments on this article.
Funding
Ke-ke Shang was supported by the National Natural Science Foundation of China (61803047), Major Project of the National Social Science Foundation of China (19ZDA149 and 19ZDA324), and Fundamental Research Funds for the Central Universities (14370119 and 14390110). Michael Small was supported by ARC Discovery Project (DP20010296).
Author contributions
B.Y. designed the research; B.Y., K.-k. S., N.C. and M.S. performed the research; B.Y., M.S and K.-k. S. analyzed the data; and B.Y., K.-k. S. and M.S. wrote the paper.
Conflict of interest
The authors declare no conflict of interest.
References
- Ferguson N. Capturing human behaviour. Nature 2007; 446: 733.[Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Funk S, Salathé M, Jansen VAA. Modelling the influence of human behaviour on the spread of infectious diseases: a review. J R Soc Interface 2010; 7: 1247–1256.[Article] [CrossRef] [PubMed] [Google Scholar]
- Funk S, Gilad E, Watkins C, et al. The spread of awareness and its impact on epidemic outbreaks. Proc Natl Acad Sci USA 2009; 106: 6872–6877.[Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wang W, Liu QH, Liang J, et al. Coevolution spreading in complex networks. Phys Rep 2019; 820: 1–51.[Article] [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Wu Q, Fu X, Small M, et al. The impact of awareness on epidemic spreading in networks. Chaos 2012; 22: 013101.[Article] [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Li K, Li C, Xiang Y, et al. Policy and newly confirmed cases universally shape the human mobility during COVID-19. Sci Open 2022; 1: 20220003.[Article] [Google Scholar]
- Granell C, Gómez S, Arenas A. Dynamical interplay between awareness and epidemic spreading in multiplex networks. Phys Rev Lett 2013; 111: 128701.[Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Granell C, Gómez S, Arenas A. Competing spreading processes on multiplex networks: Awareness and epidemics. Phys Rev E 2014; 90: 012808.[Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- de Arruda GF, Rodrigues FA, Moreno Y. Fundamentals of spreading processes in single and multilayer complex networks. Phys Rep 2018; 756: 1–59[Article] [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Sánchez-García RJ, Cozzo E, Moreno Y. Dimensionality reduction and spectral properties of multilayer networks. Phys Rev E 2014; 89: 052815.[Article] [CrossRef] [PubMed] [Google Scholar]
- Sun M, Small M, Lee SS, et al. An exploration and simulation of epidemic spread and its control in multiplex networks. SIAM J Appl Math 2018; 78: 1602–1631.[Article] [CrossRef] [MathSciNet] [Google Scholar]
- Guo Q, Lei Y, Jiang X, et al. Epidemic spreading with activity-driven awareness diffusion on multiplex network. Chaos 2016; 26: 043110.[Article] [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Kan JQ, Zhang HF. Effects of awareness diffusion and self-initiated awareness behavior on epidemic spreading - An approach based on multiplex networks. Commun Nonlinear Sci Numer Simul 2017; 44: 193–203.[Article] [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Ye Y, Zhang Q, Ruan Z, et al. Effect of heterogeneous risk perception on information diffusion, behavior change, and disease transmission. Phys Rev E 2020; 102: 042314.[Article] [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Velásquez-Rojas F, Ventura PC, Connaughton C, et al. Disease and information spreading at different speeds in multiplex networks. Phys Rev E 2020; 102: 022312.[Article] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Gray A, Greenhalgh D, Hu L, et al. A stochastic differential equation sis epidemic model. SIAM J Appl Math 2011; 71: 876–902.[Article] [CrossRef] [MathSciNet] [Google Scholar]
- McCluskey CC. Complete global stability for an SIR epidemic model with delay—Distributed or discrete. Nonlinear Anal-Real World Appl 2010; 11: 55–59.[Article] [CrossRef] [MathSciNet] [Google Scholar]
- Kabir KMA, Tanimoto J. Analysis of epidemic outbreaks in two-layer networks with different structures for information spreading and disease diffusion. Commun Nonlinear Sci Numer Simul 2019; 72: 565–574.[Article] [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bagnoli F, Lió P, Sguanci L. Risk perception in epidemic modeling. Phys Rev E 2007; 76: 061904.[Article] [CrossRef] [PubMed] [Google Scholar]
- Lazer DMJ, Baum MA, Benkler Y, et al. The science of fake news. Science 2018; 359: 1094–1096.[Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Iyengar S, Massey DS. Scientific communication in a post-truth society. Proc Natl Acad Sci USA 2019; 116: 7656–7661.[Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Scheufele DA, Krause NM. Science audiences, misinformation, and fake news. Proc Natl Acad Sci USA 2019; 116: 7662–7669.[Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zhu JH. Issue competition and attention distraction: A zero-sum theory of agenda-setting. Jism Q 1992; 69: 825–836.[Article] [Google Scholar]
- Kuehne LM, Olden JD. Lay summaries needed to enhance science communication. Proc Natl Acad Sci USA 2015; 112: 3585–3586.[Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fahy D, Nisbet MC. The science journalist online: Shifting roles and emerging practices. Journalism 2011; 12: 778–793.[Article] [CrossRef] [Google Scholar]
- Brauer F, Castillo-Chavez C, Castillo-Chavez C. Mathematical Models in Population Biology and Epidemiology. New York: Springer, 2012 [CrossRef] [Google Scholar]
- Bertozzi AL, Franco E, Mohler G, et al. The challenges of modeling and forecasting the spread of COVID-19. Proc Natl Acad Sci USA 2020; 117: 16732–16738.[Article] [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Li Q, Chen H, Li Y, et al. Network spreading among areas: A dynamical complex network modeling approach. Chaos 2022; 32: 103102.[Article] [CrossRef] [PubMed] [Google Scholar]
- Thurner S, Klimek P, Hanel R. A network-based explanation of why most COVID-19 infection curves are linear. Proc Natl Acad Sci USA 2020; 117: 22684–22689.[Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Myers SA, Sharma A, Gupta P, Lin J. Information network or social network? the structure of the twitter follow graph. In: Proceedings of the 23rd International Conference on World Wide Web, WWW ’14 Companion (Association for Computing Machinery, New York, NY, USA), p. 493-498 (2014).[Article] [Google Scholar]
- Hofman JM, Sharma A, Watts DJ. Prediction and explanation in social systems. Science 2017; 355: 486–488.[Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Small M, Cavanagh D. Modelling strong control measures for epidemic propagation with networks—A COVID-19 case study. IEEE Access 2020; 8: 109719.[Article] [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Figures
 |
Figure 1 A sketch to demonstrate our model. First, scientific information related to the disease spreads with a higher probability during an epidemic, and people who receive it will be more aware of the disease, becoming less susceptible to infection. However, while a major social event occurs during the epidemic, people’s attention will be diverted from scientific information to the social event, with lower probability for the scientific information spreading. People are therefore less likely to become aware, making them more susceptible to infection. |
| In the text | |
 |
Figure 2 The sketch of the two-layer network used in our SIR-UAU model and the schematic illustration of the SIR-UAU dynamics in that two-layer network. (A) The upper layer represents the information dissemination, where each node has two possible states: aware (A, blue nodes) or unaware (U, gray nodes). The lower layer represents the physical contact network, in which nodes have three possible states: susceptible (S, green nodes), infected (I, red nodes) or recovered (R, pink nodes). There is a one-to-one mapping between nodes in two layers, to represent the same individual in each layer. (B) The upper row presents the unaware SIR and the lower row corresponds to the aware SIR. |
| In the text | |
 |
Figure 3 Simulated comparison of (A) the number of new infected and (B) the number of new aware as a function of time step t for disease spreading under three cases: without information dissemination (blue dashed line); disease spreading with information dissemination at rate κ=0.15 (orange solid line), and disease spreading with information dissemination at rate κ=0.15 and with one event starting at time t=15 with competition effect I=0.9 and duration of 8 time steps (green dotted line). In three cases we always set the information decaying rate κ’=0.2, the infection reduction rate η=0.85, the disease spreading rate β=0.15 and the recovering rate γ=0.1. Colored bands show the 1σ confidence interval of our prediction. |
| In the text | |
 |
Figure 4 The effect of the disease spreading rate β, the information dissemination rate κ and one event on the total infected rate. (A) two-layer network of disease spreading and information dissemination without event. (B) two-layer network of disease spreading and information dissemination with one event, starting at time t=0 with competition effect I=0.9 and duration of 8. In two cases we always set the information decaying rate κ’=0.2, the infection reduction rate η=0.85 and the recovering rate γ=0.1. (C) The net effect of one event on the total infected rate, which shows the effect of the event is more significant when the information dissemination rate κ and the disease spreading rate β are both small. For the image processing, the Gaussian smoothing algorithm with σ=1.5 was used. |
| In the text | |
 |
Figure 5 Under four sets of parameters, the effect of event start time t (t∈[0,100]) and event competition effect I (I∈[0,1]) on net effect on the total infected rate of the event. In all cases we always set the information dissemination rate κ=0.15, the information decaying rate κ’=0.2 and the infection reduction rate η=0.85. For the image processing, the Gaussian smoothing algorithm with σ=1.5 was used. |
| In the text | |
 |
Figure 6 SIR-UAU two-layer network with two events to simulate from empirical data. Using data of (A) cumulative confirmed cases of United States; (B) the retweets of the COVID-19 related research papers on Twitter, depicts by the blue diamond points. The green line and the orange line correspond to the simulation results with and without the two big media events, respectively. The simulation results of the information dissemination layer are based on the hypothesis that the amount an individual will output information when entering the aware state is p=n-0.3, where n is the number of times that individual turning to aware state. Two big events are added to the two-layer network model, one is starting in the beginning, with competition effect I=0.45 and duration Δt=8, another is starting at time t=17, with I=0.87 and duration Δt=8. In the two-layer network, the disease spreading rate β=0.07, the information dissemination rate κ=0.15, the recovering rate γ=0.11, the information decaying rate κ’=0.2 and the infection reduction rate η=0.85. Color band shows the 1σ confidence interval of our prediction. |
| In the text | |
 |
Figure 7 (A) Evolution of the popularity of hashtags corresponding to two possible events and COVID-19-related information on Twitter. (B) Competition effect I calculated by popularity of the hashtags of #COVID, #Election2020, #Chinesevirus and #Chinavirus. We assume I equals to the popularity of the hashtags of the two events divided by the sum of the popularity of the hashtags of two events and the popularity of hashtag #COVID-19. (C), (D) SIR-UAU two-layer network simulated from empirical data, where the information dissemination rate is completely obtained from the hashtags of the possible two events. The diamond points depict the data of (A) cumulative confirmed cases of US; (B) the retweets of the COVID-19 related research papers on Twitter. And the green line and the orange line correspond to the simulation results with and without the two big media events, respectively. In the two-layer network, the parameters we set are consistent with the previous method, in which disease spreading rate β=0.07, information dissemination rate κ=0.15, recovering rate γ=0.11, information decaying rate κ’=0.2 and infection reduction rate η=0.85. Color band shows the 1σ confidence interval of our prediction. |
| In the text | |
 |
Figure 8 (A) Evolution of the popularity of hashtags #blm on Twitter. (B), (C) SIR-UAU two-layer network simulated from empirical data, where the information dissemination rate is completely obtained from the hashtags of the possible three events. The diamond points depict the data of (A) cumulative confirmed cases of US; (B) the retweets of the COVID-19 related research papers on Twitter. And the green line and the orange line correspond to the simulation results with and without the two big media events, respectively. In the two-layer network, the parameters we set are consistent with the previous method, in which disease spreading rate β=0.07, information dissemination rate κ=0.15, recovering rate γ=0.11, information decaying rate κ’=0.2 and infection reduction rate η=0.85. Color band shows the 1σ confidence interval of our prediction. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.

